Dana jest funkcja... mat: Dana jest funkcja o wzorze f(x) = (m² − 9)x² + (2m + 1)x − 1. Wyznacz wszystkie wartości parametru m, tak aby funkcja była malejąca w zbiorze liczb rzeczywistych.

Godzio: malejąca : a<0 m²−9 <0 m²<9 m<3 ∧ m>−3

BiebrzaFun : Godzio to nie wystarczy,to musi być prosta m²−9=0⇒m=−3 lub m=3 i 2m+1<0

	1
m<−		,więc m=−3
	2

Tola: Funkcja kwadratowa jest malejąco − rosnąca lub rosnąco −malejąca w całej dziedzinie więc aby była tylko malejaca w całej dziedzinie to musi być funkcją liniową : zatem m²−9=0 to: m= −3 v m= 3 i 2m+1 < 0 to m < −¹₂ to warunki zad będą spełnione tylko dla m = −3 bo: f(x)= 0*x² − 5x −1 = −5x −1 f(x) = −5x −1 −−−− jest malejąca w całej dziedzinie

BiebrzaFun : Zgadza się co do ety

Tola: Chyba co do "joty" Witam "agenta 07"

BiebrzaFun : Tola ,już pytałem się o to ,ale bez skutku.Spróbuję jeszcze raz .Chodzi mi o zerowy wyraz ciągu ,jeśli nie jest sprecyzowane n,n∊N.Czy a₀ jest pierwszym wyrazem ciągu?Jeśli nie,to którym jest wyrazem ,jeśli tak,to dlaczego nie używa się zapisu a₀ w ciągach ary. lub geo.? https://matematykaszkolna.pl/forum/29049.html

Tola: Do BiebrzaFun zobacz wyjaśnienie: 29417 Rozwiąż podane przeze mnie zadanie o tej sumie

BiebrzaFun : już patrzyłem wcześniej i uważam ,że to jest mało matematyczne.Chyba wcześniej opisano ciągi,a później wciągnięto 0 do N..Najwyższy czas to zmienić i ujednolicić! Zaczynam zbierać podpisy

Tola: .... namieszała ta liczba zero] Przeglądając zad. maturalne zauważyłam ,że w niektórych jest informacja: dla n≥ 1 −−−− i tu nie ma takiego problemu ale jak takiej informacji brak ; to uważam ,że do N dochodzi zero i tak wychodzi chociażby z rozwiązania tego zad. z sumą , które podałam . W przypadku nie uwzględnienia zera taki wynik nie wyjdzie ( a odp: jest D/ 780 Poczekamy na wypowiedzi Basi lub Bogdana Ja upieram się ,że zero wchodzi tu w grę Idę coś < obiad>

BiebrzaFun : suma sumarum mi chodzi oto, żeby nie było sytuacji ,że "akurat w tym ciągu" a₀=a₁ ,ale a₁ nie jest pierwszym wyrazem,tylko jest już drugim, bo pierwszy wyraz jest dla n=0 ,matematyka musi być konkretna!

Bogdan: Dobry wieczór. Włączam się do rozmowy o wyrazie ciągu oznaczonym a₀. Weźmy dowolną funkcję, np.: f(x) = 3x² − 2x + 1. Dziedziną tej funkcji jest zbiór R. Możemy narzucić jednak dziedzinę. Niech dziedziną tej funkcji będzie zbiór N₊. Wówczas f(1) = 2, f(2) = 9, ... , f(7) = 134, itd. Funkcję, której dziedziną jest zbiór liczb naturalnych dodatnich, nazywamy ciągiem. Ciąg jest funkcją, której dziedziną jest zbiór liczb naturalnych dodatnich. Zero nie należy

	1
do dziedziny tej funkcji, nie mają więc sensu wyrażenia: f(0), f(		, f(−3), itp.
	2

W funkcji będącej ciągiem wyrazem pierwszym jest f(1), wyrazem drugim jest f(2), itd. Mówiąc obrazowo, wyścig wygrywa ten zawodnik, który zajmuje na mecie pierwsze miejsce, a nie zerowe, bo takiego miejsca przecież nie ma. Przyjęta jest umowa, aby wyrazy ciągów oznaczać a₁, b₁, c₁, ... , zamiast f(1), a₂, b₂, c₂, ... , zamiast f(2), itd. Jeśli w zadaniu jest mowa o ciągu i nie ma podanego zakresu liczb naturalnych tworzących dziedzinę, to dziedziną jest zbiór liczb naturalnych dodatnich. Jeśli zadanie dotyczy ciągu określonego dla zbioru N₊, a nie dla określonego podzbioru zbioru N₊, to zbędne jest informacja, że n∊N₊ lub że n ≥ 1. Podsumowując, nie istnieje wyraz zerowy ciągu, bo zero nie należy do dziedziny funkcji będącej ciągiem.

Eta: Witam Bogdanie Ok : zawsze tak było ( zmyliło mnie zadanie i odp. do niego) zad> ( ze zb. maturalnego "matura 2010 "−− wyd. Aksjomat z Torunia) o treści: wyznacz sumę 20− tu kolejnych liczb naturalnych, które przy dzieleniu przez 4 daja resztę 3 odp. jest: S= 780 Czy odp. jest błędna?.... bo właśnie tego nie rozumiem PS: Pomyślałam ,że teraz coś nowego wprowadzono w związku z tą liczbą zero .

Rudy: Ciągi są funkcjami określonymi w dziedzinie liczb naturalnych, nie definiuje się wyrazu zerowego ciągu, pierwszym elementem ciągu jest a₁

Eta: Ok, ok, ok

Eta: Spoko Rudy

Bogdan: Witaj Eto . Mam ten zbiór, podaj namiary na zadanie z ciągiem o S = 780 (strona, nr zadania).

Eta: Str. 40 zestaw IX zad 9 oczywiście podałam zad z chochlikiem Podzielne przez 4 i dające resztę 1

AROB: No i jako poprawną odp. podają B, czyli 840.

Eta: No ja widzę ,że raz podają B ) 840 a raz D) 780 a powinna być A ) 860

Bogdan: W tym zbiorze zadań trudno znaleźć błędy. Treść zadania: suma dwudziestu początkowych kolejnych liczb naturalnych, które przy dzieleniu przez 4 dają resztę 1 wynosi:

	1
a1 = 1, r = 4, a20 = 1 + 19*4 = 77, S20 =		*20*(1 + 77) = 780.
	2

Taka odpowiedź jest podana w tym zbiorze, jest to odpowiedź D.

Nikka: dlaczego pierwszy wyraz jest równy 1 a nie 5 ?

Nikka: liczby, które przy dzieleniu przez 4 dają resztę 1 to liczby postaci 4n+1 czyli a₁ = 5 nawet gdyby n=0 to a₀ = 1 ale to nie jest liczba, która przy dzieleniu przez 4 daje resztę 1.... czy ja dobrze myślę?

Bogdan: Najmniejszą liczbą naturalną, która przy dzieleniu przez 4 daje resztę 1, to liczba 1, bo 1 : 4 = 0 + reszta 1, czyli w tym zadaniu a₁ = 1.

Nikka: ok, czyli 1 = 0*4 +1 5 = 1*4 + 1 9 = 2*4 + 1 itd.

Bogdan: Tak

Eta: Właśnie dlatego mi się "namieszało " skoro zapisałam tę liczbę jako : 4n +1 stąd bierzemy dla n= 0 i piszemy a₁ = 1 dla n=0 ( tak?) Stąd zamieszanie z tą liczbą zero

AROB:

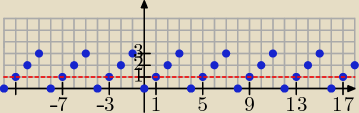
Bogdan: Liczby podzielne przez 4 dające resztę 1 to liczby postaci 4c + 1, gdzie c∊C, np.: dla c = 0 jest 1, dla c = 1 jest 5, dla c = −2 jest −7, itd. Mamy więc zbiór: {..., −11, −7, −3, 1, 5, 9, ...}. Najmniejszą liczbą naturalną jest w tym zbiorze jest liczba 1. Wzór ciągu spełniającego warunki zadania nie jest a_n = 4n + 1, a jest a_n = 4n − 3.

Gandi7: Szanowny Bogdanie prosze Cie poświęć mojemu zadanku troche uwagi mistrzu

Eta: Dzięki za wyjaśnienie Rozumiem tak: Liczby tej postaci można zapisać tak 4c +1 dla c€C ale ciąg zawierający te liczby jest postaci 4n −3 dla n€N stąd dla n=1 mamy ; a₁= 1

Rudy: ta funkcja, czyli modulo 4 jest okresowa dlatego wszystko jedno czy zapiszesz tak czy siak. Zależy od jakiego argumenty wystartujesz. Wszystkie poniższe funkcje będą miały taki sam wykres, ale tylko ostatnia odpowiada ciągowi (bo zaczyna się od 1 i ma mieć wartość 1) 4w+1=4k+5=4j−15=4n−3 bo musi być a₁=1

BiebrzaFun : wiedziałem,że jak Mistrz Forum,Guru Matematyczne,Mentor Bogdan włączy się do rozmowy,to stanie się światło Namieszałaś Eta...ale za dobre sprawowanie,wina zostaje Ci darowana.