Trapez
Bogdan:
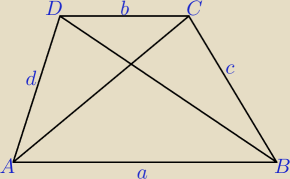
Wykaż, że w trapezie suma kwadratów długości przekątnych jest równa sumie kwadratów
długości ramion powiększonej o podwojony iloczyn długości podstaw trapezu.
|AC| = p, |BD| = q,
a, b, c, d − jak na rysunku
Wykaż, że p
2 + q
2 = c
2 + d
2 + 2ab
15 maj 23:06
kyrtap: dla kogo to Panie Bogdanie?

15 maj 23:10
Bogdan:
dla każdego
15 maj 23:11
Bogdan:
o tej porze toć to rozrywka
15 maj 23:12
kyrtap: wiadomo ale bez sił dzisiaj jestem

15 maj 23:18
kyrtap: bardziej dla naszego Metisa zadanie ^^
15 maj 23:20
Metis: Słabo u mnie z planimetrią

15 maj 23:23
kyrtap: dlatego Pan Bogdan wstawił zadanko żeby poćwiczyć

15 maj 23:25
Metis: Nigdy nie wiem od czego zacząć.
15 maj 23:46
kyrtap: tutaj chyba można pociągnąć to z podobieństwa jak tak patrzę

15 maj 23:47
Lukas:
Też kiedyś będę doktorem razem z Hugo

15 maj 23:55
15 maj 23:56
Metis: Nie wiadomo czy śmiać się, czy płakać

16 maj 00:04
Eta:
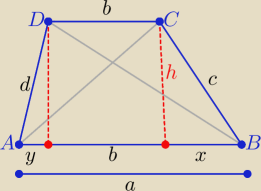
p
2=a
2+c
2−2ax
q
2=a
2+d
2−2ay
+ −−−−−−−−−−−−−−−
p
2+q
2=c
2+d
2+2a
2−2a(x+y) , x+y= a−b , a>b
p
2+q
2=c
2+d
2+2ab
c.n.u

16 maj 00:41
kyrtap: za dobra jesteś w te klocki

16 maj 00:42
b.: Też luźno myślałem nad tego typu rozwiązaniem, ale nie byłem pewien (a nie miałem ochoty
sprawdzać), czy ono nie zależy od rysunku −− tj. czy działa też dla trapezów które wyglądają
mniej trapezowo, a bardziej równoległobokowo

16 maj 00:47
Benny: Skąd to np. −2ax?

16 maj 07:35
Kacper:
Dobra to ja zaproponuje zadanko na jego podstawie

W trapezie ABCD o podstawach AB i CD przekątne przecinąją się w punkcie S i są prostopadłe.
Wykaż, że
|AC|
2+|BD|
2=(|AB|+|CD|)
2
Konkurs na "najładniejsze" rozwiązanie

16 maj 10:26
Eta:
@
Benny
"skąd to np. −2ax?" .... to zagadka dla Ciebie


16 maj 11:14
Benny: Okej

16 maj 11:28
PW: Co innego, gdyby było
−2ac·cosB,
prawda?
16 maj 11:35
Benny: PW, oczywiście, że pomyślałem na początku o twierdzeniu cosinusów. Doszedłem do
rozwiązania
Ety, ale musiałem dwa razy Pitagorasa. Chyba, że
Eta zrobiła to w
pamięci

16 maj 11:37
Eta:
Dokładnie .. Pitagoras w "pamięci"

16 maj 11:58
Godzio:
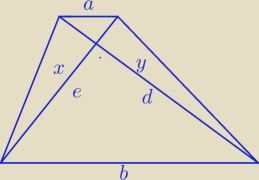
| | a | |
Skala podobieństwa trójkątów to |
| to wówczas dłuższa część przekątnej: |
| | b | |
Analogicznie druga przekątna:
Z twierdzenia Pitagorasa
x
2 + y
2 = b
2
| b2e2 + b2d2 | |
| = b2 |
| (a + b)2 | |
e
2 + d
2 = (a + b)
2
16 maj 12:03
Kacper:
Da się prościej

Konkurs nadal trwa

16 maj 12:50
Bogdan:
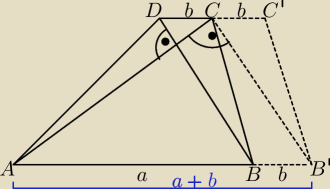
Dzień dobry.
Dla
Ety 
Podoba mi się pomysł
Kacpra z konkursem. Możemy częściej wrzucać jakieś ciekawe
zadania z informacją, że wygra ta osoba ,która przedstawi najprostsze rozwiązanie.
W zadaniu
Kacpra: |B'C| = |BD|, trójkąt ABC jest prostokątny i ... wszytko jasne
16 maj 14:44
Kacper:
Bodgan wygrał


Konkurs jest o tyle interesujący, dlatego, że rozwiązać zadania umie każdy, ale znaleść
najkrótszą drogę już tak łatwo nie jest

16 maj 14:53
Bogdan:

Powtórzę słowa kiedyś na tym forum tu
18696 zapisane:
Dojść jakoś do celu
potrafi wielu,
ale najkrótszą drogą
nieliczni mogą.
Ja mam wielką frajdę,
gdy najkrótszą drogę znajdę.
16 maj 15:11
Kacper:
Bogdan niezły z ciebie poeta

16 maj 15:36
Hugo: 
Hugo dochodzi szybko
18 maj 08:55
Hugo: ... gdyż optymalizuje GO (kod) swojego pythona.py dochodząc najszybciej i najkrótszą drogą

w końcu python jest językiem który "cechuje się przejrzystością i zwięzłością" − Wikia
kodzik z wczoraj
http://zapodaj.net/6f262c1b43fb8.png.html
18 maj 09:13
 Wykaż, że w trapezie suma kwadratów długości przekątnych jest równa sumie kwadratów
długości ramion powiększonej o podwojony iloczyn długości podstaw trapezu.
|AC| = p, |BD| = q,
a, b, c, d − jak na rysunku
Wykaż, że p2 + q2 = c2 + d2 + 2ab
Wykaż, że w trapezie suma kwadratów długości przekątnych jest równa sumie kwadratów
długości ramion powiększonej o podwojony iloczyn długości podstaw trapezu.
|AC| = p, |BD| = q,
a, b, c, d − jak na rysunku
Wykaż, że p2 + q2 = c2 + d2 + 2ab








 p2=a2+c2−2ax
q2=a2+d2−2ay
+ −−−−−−−−−−−−−−−
p2+q2=c2+d2+2a2−2a(x+y) , x+y= a−b , a>b
p2+q2=c2+d2+2ab
c.n.u
p2=a2+c2−2ax
q2=a2+d2−2ay
+ −−−−−−−−−−−−−−−
p2+q2=c2+d2+2a2−2a(x+y) , x+y= a−b , a>b
p2+q2=c2+d2+2ab
c.n.u




 W trapezie ABCD o podstawach AB i CD przekątne przecinąją się w punkcie S i są prostopadłe.
Wykaż, że
|AC|2+|BD|2=(|AB|+|CD|)2
Konkurs na "najładniejsze" rozwiązanie
W trapezie ABCD o podstawach AB i CD przekątne przecinąją się w punkcie S i są prostopadłe.
Wykaż, że
|AC|2+|BD|2=(|AB|+|CD|)2
Konkurs na "najładniejsze" rozwiązanie 






 Konkurs nadal trwa
Konkurs nadal trwa 
 Dzień dobry.
Dla Ety
Dzień dobry.
Dla Ety  Podoba mi się pomysł Kacpra z konkursem. Możemy częściej wrzucać jakieś ciekawe
zadania z informacją, że wygra ta osoba ,która przedstawi najprostsze rozwiązanie.
W zadaniu Kacpra: |B'C| = |BD|, trójkąt ABC jest prostokątny i ... wszytko jasne
Podoba mi się pomysł Kacpra z konkursem. Możemy częściej wrzucać jakieś ciekawe
zadania z informacją, że wygra ta osoba ,która przedstawi najprostsze rozwiązanie.
W zadaniu Kacpra: |B'C| = |BD|, trójkąt ABC jest prostokątny i ... wszytko jasne

 Konkurs jest o tyle interesujący, dlatego, że rozwiązać zadania umie każdy, ale znaleść
najkrótszą drogę już tak łatwo nie jest
Konkurs jest o tyle interesujący, dlatego, że rozwiązać zadania umie każdy, ale znaleść
najkrótszą drogę już tak łatwo nie jest 
 Powtórzę słowa kiedyś na tym forum tu 18696 zapisane:
Dojść jakoś do celu
potrafi wielu,
ale najkrótszą drogą
nieliczni mogą.
Ja mam wielką frajdę,
gdy najkrótszą drogę znajdę.
Powtórzę słowa kiedyś na tym forum tu 18696 zapisane:
Dojść jakoś do celu
potrafi wielu,
ale najkrótszą drogą
nieliczni mogą.
Ja mam wielką frajdę,
gdy najkrótszą drogę znajdę.

 Hugo dochodzi szybko
Hugo dochodzi szybko
 w końcu python jest językiem który "cechuje się przejrzystością i zwięzłością" − Wikia
kodzik z wczoraj
http://zapodaj.net/6f262c1b43fb8.png.html
w końcu python jest językiem który "cechuje się przejrzystością i zwięzłością" − Wikia
kodzik z wczoraj
http://zapodaj.net/6f262c1b43fb8.png.html