przestrzenie metryczne anabel: Rozważmy płaszczyznę R² z metryką euklidesową d. Niech S={x∊R² | d(x,0)=1} Niech A=N₁(S)={x∊R²| dist(x,S)<1} a)wyznaczyć A b)uzasadnić ściśle wzór z punktu a Bardzo prosze o pomoc bo kompletnie nie wiem jak się za to zabrać

anabel: up.

Godzio: A masz jakąś odpowiedź?

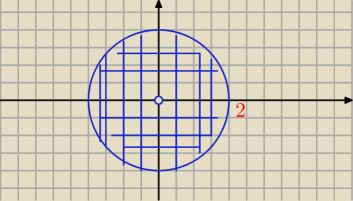
Godzio: Wyszło mi koło o promieniu 2 o środku w (0,0) bez punktu (0,0)

Godzio: Ano i bez brzegu

anabel: odpowiedzi zadnej nie mam

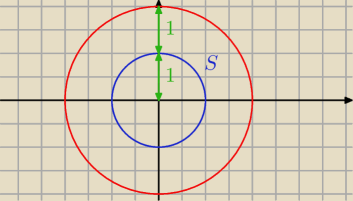
Godzio: Wychodzi, że dobrze ... a) Zbiór S to nic innego jak okrąg o środku w (0,0) i promieniu 1. A to zbiór tych punktów, że odległość jest mniejsza od 1, czyli możemy powiększyć ten okrąg o 1 (czyli mamy okrąg o środku w punkcie (0,0) i promieniu 2) i odległość będzie mniejsza od 1 jeżeli weźmiemy całe koło bez brzegu. Jedynie wykluczamy środek, którego odległość od S jest równa 1 (a szukamy < 1). b) Ścisłe wyliczenie: d(s,0) = √s₁² + s₂² = 1 ⇔ s₁² + s₂² = 1 dist(x,S) = inf_s∊Sd(x,s) = inf_s∊S√(x₁ − s₁)² + (x₂ − s₂)² = = inf_s∊S√x₁² + x₂² + s₁² + s₂² − 2x₁s₁ − 2x₂s₂ = = inf_s∊S√x₁² + x₂² + 1 − 2x₁s₁ − 2x₂s₂ Rozważamy funkcję f(s₁,s₂) = − 2x₁s₁ − 2x₂s₂ pod warunkiem, że s₁² + s₂² = 1 Szukamy jej minimum. G(s₁,s₂) = s₁² − s₂² − 1 F(s₁,s₂) = − 2x₁s₁ − 2x₂s₂ + λs₁² + λs₂² − λ

	x1
Fs1 = − 2x1 + 2λs1 = 0 ⇒ s1 =
	λ

	x2
Fs2 = − 2x2 + 2λs2 = 0 ⇒ s2 =
	λ

	x12 + x22
Fλ = s12 + s22 − 1 = 0 ⇒		= 1 ⇒ λ = √x12 + x22
	λ2

	x1		x2
s1 =		oraz s2 =
	√x12 + x22		√x12 + x22

Liczymy drugie pochodne F_s1s1 = 2λ F_s1s2 = F_s2s1 = 0 F_s2s2 = 2λ F_λλ = 0 F_λs1 = F_s1λ = 2s₁ F_λs2 = F_s2λ = 2s₂ Tworzymy Hesjan i liczymy wyznacznik 0 2s₁ 2s₂ 2s₁ 2λ 0 = − 8s₂²λ − 8s₁²λ = −8λ(s₁² + s₂²) = − 8λ = 2s₂ 0 2λ = − 8√x₁² + x₂² < 0 zatem w punkcie (s₁,s₂) jest osiągnięte minimum warunkowe, a stąd mamy

	x1		x2
s1 =		oraz s2 =		i
	√x12 + x22		√x12 + x22

inf_s∊S√x₁² + x₂² + 1 − 2x₁s₁ − 2x₂s₂ = √x₁² + x₂² + 1 − 2x₁²/√x₁²+x₂² − 2x₂²/√x₁² + x₂² = √x₁² + x₂² + 1 − 2√x₁² + x₂² = √(√x₁² + x₂² − 1)² = |√x₁² + x₂² − 1| < 1 ⇔ 0 < √x₁² + x₂² < 2 /² 0 < x₁² + x₂² < 4 −− a to jest właśnie koło o promieniu 2 bez brzegu i środka

Godzio:

Godzio: Jeżeli masz jakieś pytania to postaraj się je zadać w ciągu ~ 15 min bo dzisiaj dopiero w nocy będę mógł coś pomóc

anabel: częśc a) jeszcze zrozumiałam, jesli chodzi o b) nie rozumiem nic...

anabel: a powiedziałbys mi jak liczyc zadania w takim stylU: https://matematykaszkolna.pl/forum/292979.html

anabel: a nad tym jeszcze posiedze to moze zrozumiem

Godzio: dist(x,S) −− odległość od zbioru, jest zdefiniowana jako infimum po s ∊ S z odległości między x i s. Rozpisujemy sobie wiedząc, że jest to metryka euklidesowa (czyli suma kwadratów pod pierwiastkiem − wzorek z liceum). Chcę policzyć minimum pierwiastka, ale mogę się skupić tylko i wyłącznie na części zawierającej s₁ i s₂, bo reszta to stałe, stąd taka funkcja, a nie inna Warunkiem jest należenie do zbioru S czyli spełniona jest zależność s₁² + s₂² = 1. To będzie nasz warunek. O ekstremach warunkowych możesz przeczytać tutaj: http://www.wzr.pl/bwz/files/file/MD2%20-%20Warunkowe%20ekstrema%20funkcji.pdf Myślę, że całkiem dobrze jest pokazane krok po kroku Działaj!

anabel: dzięki za pomoc