geometria analityczna olekturbo: problem z zadankiem z geo. analitycznej Wyznacz rownanie prostej przechodzacej przez punkt P(2,6) tworzacej z dodatnimi polosiami ukladu wspolrzednych trojkat o Polu = 24.

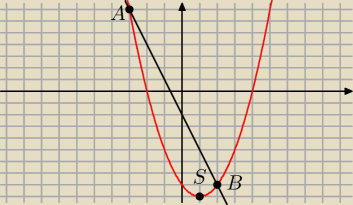
olekturbo: i jeszcze drugie jakby ktoś miał ochotę: Prosta y+3x+2 = 0 przecina parabolę y = x²−2x−8 w pkt A i B. a) oblicz pole i obwód trojkąta ABS gdzie S jest wierzchołkiem paraboli I o ile z tym podpunktem nie miałem kłopotu to w tym tylko obliczyłem R, a nie wiem jak znaleźć środek okręgu b) napisz równanie okręgu opisanego na tym trójkącie dla ułatwienia: A(−3,7) B(2,−8) S(1,−9)

Tadeusz: (x_s+3)²+(y_s−7)²=r² (x_s−2)²+(y_s+8)²=r² (x_s−1)²+(y_s+9)²=r² i licz

olekturbo: dzieki

5-latek: https://matematykaszkolna.pl/strona/541.html czytamy ostatnie zdanie tutaj i liczmy srodek okręgu opisanego na tym trojkacie

tester: ta prosta wyszła mi y =−3x+12, taka jest odp?

Tadeusz: To pierwsze zadanie możesz policzyć "różnymi ścieżkami" Kiedyś liczyłem je już tu wykorzystując równanie prostej w postaci odcinkowej. A można również tak: Piszesz równanie pęku prostych przez punkt P=(2,6) y−6=a(x−2) ⇒ y=ax−2a+6 Liczysz punkty przecięcia się z 0x i 0y dla x=0 y=6−2a

	2a−6
dla y=0 0=ax−2a+6 ⇒ ax=2a−6 ⇒ x=
	a

	2a−6
Z pola trójkąta (6−2a)		=48 i z tego a=−3
	a

Twoja prosta zatem to y=−3x+12

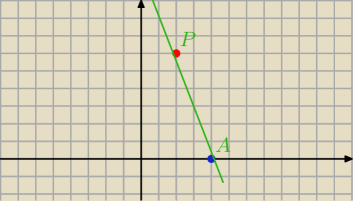
5-latek: Prosta ta będzie przechodzić przez punkty P=(2,6) i A=(4,0)

y−y1		y2−y1
	=
xx1		x2−x1

y−6		−6
	=
x−2		2

y−6
	=−3
x−2

−3x+6=y−6 −3x+12=y Masz wiec dobrze

olekturbo: skad wiadomo ze bedzie przechodzic przez punkt A(4,0)

tester: Dokładnie takim sposobem jak Tadeusz robiłem