. Kasia: zadanie maturalne BŁAGAM MĘCZE SIĘ Z TYM OD GODZINY Dany jest trójkąt ABC. Punkty D,E leżą odpowiednio na bokach AB i AC tak, że ADB=1:2 i AE:EC=2:1. Punkt F jest punktem przecięcia prostych CD i EB. Wyznacz jaką część pola ABC stanowi czworokąt ADFE.

YushokU: Robione było wielokrotnie na tym forum. https://matematykaszkolna.pl/forum/280787.html

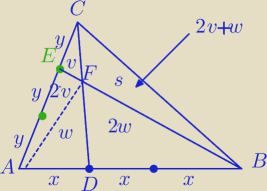Mila: P− pole ΔABC

	1		1
PΔADC=		P⇔3v+w=		P
	3		3

	1		1
PΔCEB=		P⇔v+s=		P
	3		3

===============================⇔3v+w=v+s⇔2v+w=s 2v+v+2v+w+w+2w=P⇔5v+4w=P

	1		1
3v+w=		P⇔w=		P−3v
	3		3

	1
5v+4*(		P−3v)=P
	3

	1
5v−12v=−		P
	3

	1
7v=		P
	3

	1		1		3		4
v=		P i w=		P−		P=		P
	21		3		21		21

	6		2
PADFE=2v+w=		P=		P
	21		7

	2
PADFE=		P
	7

=============== Posprawdzaj rachunki

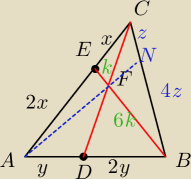YushokU: I jeszcze metoda ode mnie P_ABC=P

	P
PADC=
	3

	P
PBCE=
	3

Jest tak dlatego, że trójkąty ADC i DBC mają wspólną wysokość, tak samo jak trójkąty BCE i ABE Następnie. Z tw. Cevy:

EC		AD		BN
	*		*		=1
EA		DB		NC

BN		4
	=
NC		1

Potem: Z tw. van Aubel'a

BF		BD		BN
	=		+
FE		DE		NC

BF		6
	=
FE		1

ΔAFC iΔFBC mają wspólną wysokość.

	1		P
PEFC=		*PBCE=
	7		21

	6P		2P
PADFE=PADC−PECF=		=
	21		7

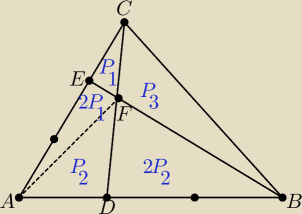Bogdan: Kiedyś pokazałem na forum takie rozwiązanie tego zadania: P₁, P₂, P₃ − pola trójkątów. 2*P_ADC = P_DBC ⇒ 2(P₁ + 2P₁ + P₂) = 2P₂ + P₃ ⇒ P₃ = 6P₁ 2*P_EBC = P_ABE} ⇒ 2(P₁ + P₃) = 2P₁ + P₂ + 2P₂ 2(P₁ + 6P₁) = 2P₁ + 3P₂ ⇒ P₂ = 4P₁ Pole trójkąta ABC: P = P₁ + 2P₁ + P₂ + 2P₂ + P₃ = 21P₁ Pole czworokąta ADFE: 2P₁ + P₂ = 6P₁

PABC		6P1		2
	=		=
PADFE		21P1		7

YushokU: @Bogdan Ładniejszego już chyba być nie może