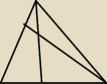
 W trójkącie ABC punkty D, E leżą odpowiednio na bokach AB i AC tak, że |AD| : |DB| = 1:2 oraz
|AE| : |EC| = 2:1. wyznacz jaka czesc pola trojkata abc stanowi pole czworokata ADFE
W trójkącie ABC punkty D, E leżą odpowiednio na bokach AB i AC tak, że |AD| : |DB| = 1:2 oraz
|AE| : |EC| = 2:1. wyznacz jaka czesc pola trojkata abc stanowi pole czworokata ADFE

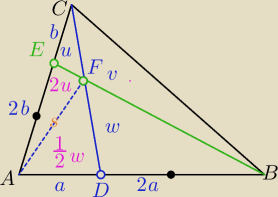 P=PΔABC
P=PΔABC
| 1 | ||
PΔADC=s+u= | P | |
| 3 |
| 1 | ||
PΔBEC=u+v= | P⇔s+u=u+v⇔ | |
| 3 |
| 1 | ||
PΔAFD= | w podobne uzasadnienie | |
| 2 |
| 1 | ||
s=2u+ | w | |
| 2 |
| 1 | 1 | |||
u+2u+ | w= | P⇔ | ||
| 2 | 3 |
| 1 | 1 | |||
3u+ | w= | P | ||
| 2 | 3 |
| 1 | 2 | |||
2u+ | w+w= | P | ||
| 2 | 3 |
| 1 | 1 | |||
3u+ | w= | P | ||
| 2 | 3 |
| 3 | 2 | |||
2u+ | w= | P | ||
| 2 | 3 |
| 1 | ||
u= | P | |
| 21 |
| 8 | ||
w= | P | |
| 21 |
| 1 | 5 | |||
s=u+ | w= | P | ||
| 2 | 21 |
| 5 | ||
PADFE= | PΔABC | |
| 21 |
| Pc.AEFD | a+2b | |||
to z warunków zadania(*) | = | =? | ||
| PΔABC | 3a+3b+c |
| PΔACD | 1 | PΔABE | 1 | ||||
= | i | = | ⇔ | ||||
| PΔBCD | 2 | PΔCBE | 2 |
| 3b+a | 1 | c+b | 1 | |||||
⇔ | = | i | = | ⇔ c+2a=6b+2a i 3a+2b=2c+2b ⇔ | ||||
| c+2a | 2 | 3a+2b | 2 |
| Pc.AEFD | 4b+2b | 6b | 2 | ||||
= | = | = | , | ||||
| PΔABC | 12b+3b+6b | 21b | 7 |

| 1 | 1 | 1 | 8 | 2 | 4 | |||||||
s=2u+ | w=2* | P+ | * | P= | P+ | P= | ||||||
| 2 | 21 | 2 | 21 | 21 | 21 |
| 6 | 2 | |||
= | P= | P | ||
| 21 | 7 |

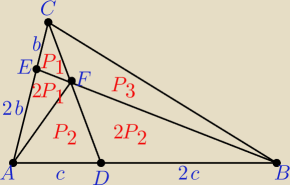 albo tak:
P1, P2, P3 − pola trójkątów
2(P1 + 2P1 + P2) = P3 +2P2 ⇒ 6P1 + 2P2 = P3 + 2P2 ⇒ P3 = 6P1
2(P1 + P3) = 2P1 + P2 + 2P2 ⇒ 2P1 + 2*6P1 = 2P1 + 3P2 ⇒ P2 = 4P1
albo tak:
P1, P2, P3 − pola trójkątów
2(P1 + 2P1 + P2) = P3 +2P2 ⇒ 6P1 + 2P2 = P3 + 2P2 ⇒ P3 = 6P1
2(P1 + P3) = 2P1 + P2 + 2P2 ⇒ 2P1 + 2*6P1 = 2P1 + 3P2 ⇒ P2 = 4P1
| PADFE | 2P1 + P2 | 6P1 | 2 | ||||
= | = | = | |||||
| PABC | 3P1 + 3P2 + P3 | 21P1 | 7 |