 Podaję inny sposób rozwiązania z wykorzystaniem wektorów
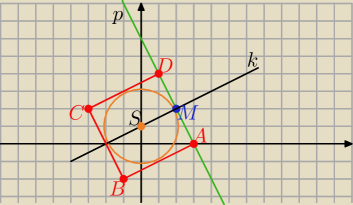
o : x2+y2−2y−4=0 ⇒ S(0,1), r=√5
prosta p = DA : 2x+y−6=0 to prosta k ⊥p i S∊k
ma równanie : 1(x−xS)−2(y−yS)=0 ⇒ k: x−2y+2=0
rozwiązując układ równań prostych k i l
otrzymujemy współrzędne punktu styczności M (2,2)
→ →
DA= [2,1] to AB=[ −1,2]
zatem A : (M(2,2)−[−1,2]) = (2+1, 2−2)= (3, 0)
D : (M(2,2)+[−1,2])= (1,4)
B: (2xS−xD, 2yS−yD) = (−1,−2)
C: (2xS−xA, 2yS−yA)= (−3,2)
Podaję inny sposób rozwiązania z wykorzystaniem wektorów
o : x2+y2−2y−4=0 ⇒ S(0,1), r=√5
prosta p = DA : 2x+y−6=0 to prosta k ⊥p i S∊k
ma równanie : 1(x−xS)−2(y−yS)=0 ⇒ k: x−2y+2=0
rozwiązując układ równań prostych k i l
otrzymujemy współrzędne punktu styczności M (2,2)
→ →
DA= [2,1] to AB=[ −1,2]
zatem A : (M(2,2)−[−1,2]) = (2+1, 2−2)= (3, 0)
D : (M(2,2)+[−1,2])= (1,4)
B: (2xS−xD, 2yS−yD) = (−1,−2)
C: (2xS−xA, 2yS−yA)= (−3,2)