Analityczna Mania : Proszę o pomoc! nic nie wychodzi.. W prostej o równaniu 2x+y−6=0 zawiera się bok kwadratu opisanego na okręgu o równaniu x²+y²−2y−4=0 . Oblicz współrzędne wierzchołków tego kwadratu. Zrobiłam z tych równań układ równań, rozwiązałam i wyszło mi że x=2 i y=2 co jest bzdurą. Mam promień i środek (0,1). Stoję, czy ktoś mógłby pomóc?

bart: zrob z tego uklad rownan.. wyjda Ci dwa rozwiazania i sa to srodki stycznych do okregow, ktore sa jednoczesnie srodkami bokow kwadratu. nastepnie zrob to samo ale z prosta prostopadlą..

dero2005: dobrze Ci idzie. Znalazłaś punkt styczności prostej i okręgu

Mania : zrobiłam i delta mi wychodzi 0 Jedno rozwiązanie ? Coś nie tak,

dero2005: powinien Ci wyjść jedno rozwiązanie, bo to jest punkt styczności prostej z okręgiem a ta prosta ma jeden punkt styczności

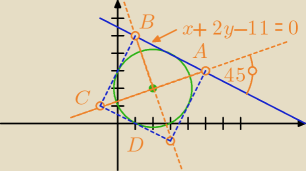
dero2005: Przykładowe zadanie Prosta o równaniu x+2y−11 = 0 zawiera bok kwadratu, w który wpisany jest okrąg o równaniu (x−2)² + (Y−2)² = 5 . Znajdź współrzędne wierzchołków kwadratu. Przykładowe rozwiązanie − liczymy współczynnik kierunkowy prostej x+2y−11 = 0 y = −¹₂x+¹¹₂ a = −¹₂ − liczymy współrzędne środka okręgu (x−x_o)²+(y−y_o)² = 5 (x−2)²+(y−2)² = 5 x_o = 2 y_o = 2 S=(2,2) −liczymy współczynniki kierunkowe prostych zawierających przekątne kwadratu(przechodzących przez punkt S) czyli przecinających prostą pod kątem 45^o

	a1−a2
tgφ = |		| tg 45o = 1 a1 = −12
	1+a1*a2

a1−a2		(a1−a2)
	= 1 lub −		= 1
1+a1*a2		1+a1*a2

a₂ = −3 lub a₂ = ¹₃ −liczymy równania tych prostych przechodzących przez punkt S(2,2) y_BD = a₂(x−x_S)+y_S y_AC = a₂(x−x_S)+y_S y_BD = −3(x−2)+2 y_AC = ¹₃(x−2)+2 y_BD = −3x + 8 y_AC = ¹₃x + ⁴₃ − liczymy punkt B y_BD = y_AB 3x+8 = −¹₂x+¹¹₂ x = 1 y = 5 B(1,5) −liczymy punkt A y_AC = y_AB ¹₃x+⁴₃ = −¹₂x+¹¹₂ x = 5 y = 3 A(5,3) −liczymy punkt C. Ponieważ punkt S jest środkiem odcinków AC i BD zastosujemy wzór na środek odcinka

	xA+xC		yA+yC
S=(		,		) = (2,2)
	2		2

x_C +x_A = 4 y_C+y_A = 4 x_C = −1 y_C = 1 C(−1,1) liczymy punkt D (jak wyżej) x_D = 3 y_D = −1 D(3,−1)