wykaż, żę
ks: Wykaż, że jeśli jeden z kątów trójkąta ma miarę 60 stopni, to długość przeciwległego boku jest
√3 razy większa od promienia okręgu opisanego na tym trójkącie.
1 maj 19:16
Vi__:
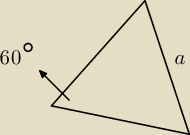
Musisz udowodnić, że a =
√3R
1 maj 19:21
kix:
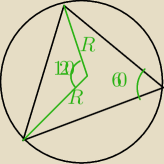
1 maj 19:22
ks: nie wiem w ogóle jak ruszyć, czy ktoś mógłby to rozwiązać? proszę

1 maj 19:30
kix:
sposób kolegi piętro wyżej jest prawie rozwiązaniem tego zadania, wyznacz a, wstaw wartość
sin60 i samo wyjdzie, albo zastosuj tw. cosinusów.

1 maj 19:37
1 maj 19:41
ks: tyle wystarczy, czy cos jeszcze trzeba obliczyc?
a / √3/2 = 2R /x √3/2
a= 2R x √3/2
a= R √3
1 maj 20:12
kix:
styknie nawet na szóstkę

1 maj 20:13
ks: haha wspaniale geniusze !

podziękował! poproszę 7++

1 maj 20:20
 Musisz udowodnić, że a = √3R
Musisz udowodnić, że a = √3R




 podziękował! poproszę 7++
podziękował! poproszę 7++ 