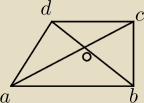
 Przekątna trapezu prostokątnego ABCD przecinają się w punkcie O. (rysunek obok) Mają one dane
IABI=8, IBCI=6, ICD=6. Oblicz obwód trójkąta ABO oraz pole trójkąta DAO.
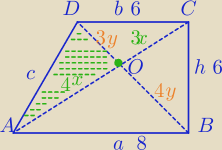
Przekątna trapezu prostokątnego ABCD przecinają się w punkcie O. (rysunek obok) Mają one dane
IABI=8, IBCI=6, ICD=6. Oblicz obwód trójkąta ABO oraz pole trójkąta DAO.
| 8 | 4 | |||
ΔABO∼ΔDCO (cecha kkk) w skali k= | = | |||
| 6 | 3 |
| 10 | ||
x= | ||
| 7 |
| 4*10 | 40 | |||
|AO|= | = | |||
| 7 | 7 |
| 6√2 | ||
y= | ||
| 7 |
| 24√2 | ||
|OB|= | ||
| 7 |
| 24√2 | 40 | 96+24√2 | ||||
ObwódΔABO=8+ | + | = | ||||
| 7 | 7 | 7 |
| 1 | ||
PΔDCA= | *6*6=18 | |
| 2 |
| PΔAOD | 4 | ||
= | |||
| PΔDOC | 3 |


| 4 |
| |||||||||||||||||||||||
= | ||||||||||||||||||||||||
| 3 |
|
| 4 | 240 √2 | 180 √2 | ||||
= | : | |||||
| 3 | 7 | 7 |
| 240 | ||
3 * | = 4 * {180}{7} | |
| 7 |
 Czyli będzie:
Czyli będzie:
| 18 | 1 | |||
18 = 6 * | * | + PΔDOC | ||
| 7 | 2 |
| 54 | ||
18 = | + PΔDOC | |
| 7 |
| 126 | 54 | |||
PΔDOC = | − | |||
| 7 | 7 |
| 72 | ||
PΔDOC = | ||
| 7 |
| k*P | ||
P(trapezu)=(k+1)2*P2 i P3=k*P2 , P(AOD)= | ||
| (k+1)2 |
| 4 | 72 | |||
dla P=42 i k= | ⇒ P(AOD)= | |||
| 3 | 7 |