Optymalizacja
imprimatur: Przygotowując książkę do druku przyjęto, że na każdej stronie tekst ma zajmować powierzchnię
150 cm2, marginesy dolny i górny mają być równe po 3 cm, a prawy i lewy po 2 cm. Oblicz,
jakie powinny być wymiary strony, aby na druk tej książki zużyć jak najmniej papieru.
1 maj 02:16
Vuks:
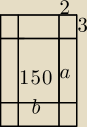
a, b > 0
P
c = 2*3*b + 2*2*a + 4*2*3 //Pole całkowite strony
| | 150 | | 900 | |
Pc = 6* |
| + 4*a + 24 = |
| + 4*a + 24 //Podstawienie za b |
| | a | | a | |
P
c jest funkcją jednej zmiennej (a), muszę obliczyć najmniejszą dodatnią
wartość. W tym celu obliczam pochodną (
359):
| | 900 | | 225 | |
Pc' = − |
| + 4 = 4(1 − |
| ) |
| | a2 | | a2 | |
Z tego wynika, że pochodna jest równa 0 dla a = 15 ⋁ a = −15 (sprzeczne, bo a > 0)
Z pierwszego równania wyznaczam b.
Nie wiem, czy przy tej pochodnej nie powinno się jakoś udowodnić,
że to jest najmniejsza wartość a nie np. największa.
Mam nadzieję że zrobiłem dobrze i pomogłem

1 maj 09:06
Janek191:
| | 150 | |
a*b = 150 ⇒ b = |
| , a > 0 i b > 0 |
| | a | |
P
c = ( b + 4)*( a + 6) = a*b + 6 b + 4 a + 24 = 150 + 24 + 4a + 6 b
| | 900 | |
Pc(a) = 174 + 4 a + |
| |
| | a | |
więc
| | 900 | | 900 | |
P'c (a) = 4 − |
| = 0 ⇔ |
| = 4 ⇔ 900 = 4 a2 ⇔ a2 = 225 ⇔ |
| | a2 | | a2 | |
⇔ a = 15
=========
| | 1 800 | |
P''c( 15) = |
| > 0 więc funkcja Pc (a) osiąga dla a = 15 |
| | 153 | |
minimum.
zatem strona ma wymiary 21 cm na 14 cm.
==================================
1 maj 09:51
Vuks: Aaaaa, teraz zauważyłem, że przy polu całkowitym zapomniałem o dodaniu pola tekstu, czyli 150.
Na maturze pewnie punkt albo dwa by poszły w diabły...

1 maj 09:59
imprimatur: Janek191, Vuks! Jesteście wielcy! Dziękuje serdecznie

1 maj 11:45
 a, b > 0
a, b > 0


