MATURA kyrtap: MATURA ARKUSZ 1

	π
1. W ciągu arytmetycznym (an) trzeci wyraz jest równy		, a szósty wyraz tego ciągu jest
	2

równy π. Oblicz wartość wyrażenia cosa₅ − sina₇.(5 pkt) 2. Przekształcenie płaszczyzny, które punktowi A o współrzędnych (3,−3) przyporządkowuje punkt

	⎧	x' = 2x + 2
A' taki, że A' = (x',y'), gdzie	⎨		, jest jednokładnością o środku w
	⎩	y' =2y+1

punkcie P = (−2,−1). Wyznacz współrzędne A' oraz skalę tej jednokładności. Napisz równanie obrazu okręgu x²+y²−6x = 0 w tej jednokładności. (7 pkt) 3. Wykres funkcji f(x) = 2^x przekształcono i otrzymano wykres funkcji g takiej że g(x) = −f(x−2)+2. a)Narysuj wykres tej funkcji f i wykres funkcji g. b) Podaj liczbę rozwiązań równania |g(x)| = m w zależności od parametru m. (6 pkt) 4. Czworościan foremny o krawędzi a przecięto płaszczyzną wyznaczoną przez krawędź boczną i wysokość czworościanu. Wyznacz pole tego przekroju. 5. W pudełku jest n żetonów o wartości 1 zł, n+2 żetonów o wartości 2 zł oraz 2n żetonów o wartości 3 zł. Prawdopodobieństwo zdarzenia A wylosowania z pudełka dwóch żetonów o łącznej

	1
wartości 4 zł jest równe		. Oblicz, ile żetonów każdego rodzaju jest w pudełku.(7 pkt)
	3

	sinα
6. Dla kątów α, β, γ trójkąta ABC zachodzi związek		= 2cosγ. Uzasadnij, że trójkąt
	sinβ

ABC jest równoramienny. (5 pkt) 7. Oblicz, dla jakich wartości parametru m różnica pierwiastków równania (m−2)x² − (m−4)x − 2 =0 jest równa 3. (6 pkt) 8. Wykaż, że jeśli równanie postaci x³ + ax + b = 0 ma pierwiastek podwójny, to 4a³ + 27b² = 0. (6 pkt)

	cosx
9. Rozwiąż równanie 2sin2x +		= 4cosx, jeśli x∊<0,2π>. Ze zbioru rozwiązań tego
	sinx

równania losujemy bez zwracania dwie liczby. Oblicz prawdopodobieństwo zdarzenia, że co

	π
najmniej jedno z wylosowanych rozwiązań jest wielokrotnością liczby		.
	2

Braun: Można robić tak ?

kyrtap: TYLKO MATURZYŚCI

Braun: A skąd wiesz, że nim nie jestem ! Albo może poprawiam ? Dyskryminacja...

kyrtap: odpowiedzi jutro z rańca (czytaj 12)

Wazyl: 8 Np tak: x₁+2x₂=0 ⇒x₁=−2x₂ x₂²+2x₁x₂=a ⇒ −3x₂²=a ⇒ −27x₂⁶=a³ ⇒ −4*27x₂⁶=4a³ x₁x₂²=−b ⇒ 2x₂³=b ⇒ 4x₂⁶=b² ⇒ 4*27x₂⁶=27b² Dodając równania stronami otrzymujemy: 4a³+27b²=0 cnw. 7 Zał: m≠2 Δ>0 x₁*x₂=... x₁+x₂=... x₁−x₂=3 9 cos przed nawias. 6 sin(π−(β+γ))=sin(β+γ)=sinβcosγ+sinγcosβ sinβcosγ+sinγcosβ=2sinβcosγ ⇒ sinγcosβ−sinβcosγ=0 ...

Benny: To pierwsze 5 pkt? To albo ja coś źle zrobiłem albo nie jest trudne.

	π
a3=
	2

a₆=π

	π
3r=
	2

	π
r=
	6

	5π
a5=
	6

	7π
a7=
	6

	5π		7π		π		π		1−√3
cos		−sin		=−cos		+sin		=
	6		6		6		6		2

Benny: 2. A'(8;−5) k=2 O': (x−8)²+(y−1)²=36

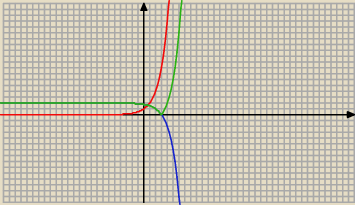
Benny: 3. Czerwona − f(x) Niebieska i ta część zielonej co leci w lewo : g(x) zielona : |g(x)| Liczba rozwiązań: m∊(2;+∞) ∪ {1} − jedno rozwiązanie m∊(0;2) − dwa rozwiązania m∊(−∞;0) − brak rozwiązań

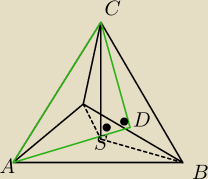
Benny: Przekrój ΔADC Podstawa przekroju jest wysokość podstawy.

	a√3
ha=
	2

	1	a√3		a√3
H2+(			)2=(		)2
	3	2		2

	1
H=		*a√3
	3

	a√3		1		1
P=		*		*a√3*
	2		3		2

	1
P=		*a2
	4

kyrtap:

	1−√3
1.		(czyli ok )
	2

2. ładnie 3. brak rozwiązań gdy m∊ (−∞,0) 1 rozwiązanie gdy m = 0 lub m∊<2,∞) 2 rozwiązania gdy m∊(0,2)

	a2√3
4. P =
	4

5. czekam 7.czekam na wyznaczenie parametru m 8 ładnie

Benny:

	√6
Błąd H=		a
	3

	1
P=		a2√2
	4

kyrtap: ja sam zaraz przeliczę bo w tych odpowiedziach mogą być błędy

Benny: 7. Wyszło mi m=3 lub m=6

Adam: Co to za matura? Skąd to?

Kacper: Benny w tym roku matura?

Benny: Tak, kurde coś mi to m=6 nie pasuje jak wstawiam do równania.

kyrtap: z CKE

Kacper: Bo m=6, to błędna wartość

kyrtap: jak dzisiaj nie rozwiążecie jej całej jutro nie wstawię kolejnego arkusza a mam ich 6

Kacper: Kyrtap napisz do mnie na gadu

Benny: Kacper zajrzyj tu https://matematykaszkolna.pl/forum/291726.html

Benny: 5. 1zl − 1 moneta 2zl − 3 monety 3zl − 2 monety

Aerodynamiczny: 9.x∊{^π₆;^π₂;^5π₆;^3π₂} i prawdopodobieństwo zdarzenia, że co najmniej jedno z wylosowanych rozwiązań jest wielokrotnością liczby jest równe ²₃

Aerodynamiczny: jest wielokrotnością liczby ^π₂*, zjadło mi ^π₂

YushokU:

	1−√3
1.
	2

2.A'(8,−5) Jednokładność o skali k=2 Równanie okręgu to: (x−6)²+y²=36 3.g(x)=−2^x−2+2 0 rozwiązań − m∊(−∞;0) 1 rozwiązanie − m∊{0}U<2;+∞) 2 rozwiązania − m∊(0,2)

	a2√2
4.P=
	4

5.żetony 1złotowe−1 żetony 2złotowe−3 żetony 3złotowe−2 6.Rysuję trójkąt dowolny o wierzchołkach ABC i oznaczam go standardowo: na przeciwko A−a na przeciwko B−b na przeciwko C−c

a		b		a		sinα
	=		⇒		=
sinα		sinβ		b		sinβ

	a
czyli		=cosγ
	2b

Z twierdzenia cosinusów.

	a
c2=a2+b2−2ab
	2b

c²=b² c=b Ramiona przyległe do kąta α są równe, więc trójkąt jest równoramienny.

	3
7.m∊{		;3}
	2

	π		π		5π		3π
8.Rozwiązania to:		,		,		,
	6		2		6		2

	5
Prawdopodobieństwo wynosi:
	6

Tak mi to powychodziło. Maturka moim zdaniem niezbyt trudna i nie pod 2015

Kacper: Co znaczy nie pod 2015?

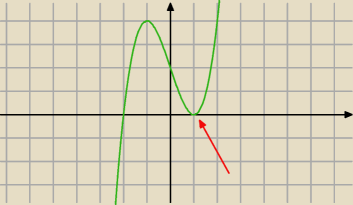
YushokU: Łoj, zgubiłem zadanie, będę pisał na bieżąco. 8. Nie chce mi się tego rozpisywać, ale skoro jest podwójny to ta funkcja tak jakby odbija. Czyli oznacza to, że jeśli ma w tym punkcie pierwiastek, to ma też w tym miejscu ekstremum. Liczę pochodną. f'(x)=3x²+a f'(x)=0 f(x)=0

	−a
3x2+a=0⇒x2=		− podstawiam do drugiego równania
	3

x³+ax+b=0

−a
	x+ax+b=0
3

−ax+3ax+3b=0 2ax+3b=0

	−3b
x=		− już widać, że powinno wyjść, podstawiam do równania z pochodnej
	2a

	−3b
3(		)2+a=0
	2a

	9b2
3(		+a=0 − mnożę przez 4a2
	4a2

27b²+4a³=0 − co należało wykazać

YushokU: @Kacper Wiem, że matematyka to matematyka, ale po zrobieniu x arkuszy 2015 to widzę, że tak jakby jest zwracana na co innego uwaga niż rok,dwa czy trzy temu. To takie moje odczucie, bo jak robiłem jakieś arkusze 2014,2013 to właśnie miałem wrażenie że są inne i ten jest do nich podobny.