 1)
Rzucamy pięć razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia p
polegającego na tym, że iloczyn liczb oczek otrzymanych we wszystkich pięciu rzutach będzie
równy 16
2)
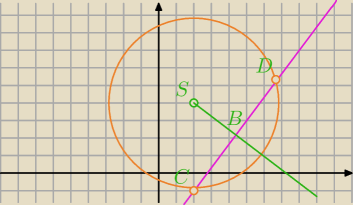
Prosta o równaniu 4x−3y−11=0 przecina w punktach C i D okrąg o środku S(2;4) . Długość odcinka
CD jest równa 8 . Wyznacz równanie tego okręgu.
3)
Trapez równoramienny ABCD o podstawach AB i CD i obwodzie równym L jest opisany na okręgu.
Oblicz pole trapezu wiedząc, że przekątna trapezu jest dwa razy dłuższa od ramienia.
1)
Rzucamy pięć razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia p
polegającego na tym, że iloczyn liczb oczek otrzymanych we wszystkich pięciu rzutach będzie
równy 16
2)
Prosta o równaniu 4x−3y−11=0 przecina w punktach C i D okrąg o środku S(2;4) . Długość odcinka
CD jest równa 8 . Wyznacz równanie tego okręgu.
3)
Trapez równoramienny ABCD o podstawach AB i CD i obwodzie równym L jest opisany na okręgu.
Oblicz pole trapezu wiedząc, że przekątna trapezu jest dwa razy dłuższa od ramienia.
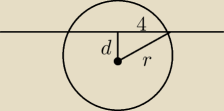 2) oblicz odległość S od prostej (d)
r2 = d2 + 42 → oblicz: r
2) oblicz odległość S od prostej (d)
r2 = d2 + 42 → oblicz: r
| 5! | 5! | 5! | ||||
IAI = | + | + | ||||
| 2!*2! | 4!*1! | 2!*3! |
| 4 | 11 | |||
Prosta y= | x− | |||
| 3 | 3 |
| 3 | 3 | |||
y−4=− | (x−2) ⇒ y=− | x+5,5 | ||
| 4 | 4 |
 Jednak dalej mam problem z 1 i 3 bo w 1 złe wyniki wychodzą przynajmniej mi
Jednak dalej mam problem z 1 i 3 bo w 1 złe wyniki wychodzą przynajmniej mi 
| 5 | ||
źle liczysz ... bo z mojego równania wychodzi: |  | |
| 864 |
| 45 | ||
IΩI = 7776 | = U{5}864} | |
| 7776 |
| 5! | 4*5*6 | ||
= | = 30 | ||
| 2!*2! | 2*2 |
| 5! | 4!*5 | ||
= | = 5 | ||
| 4!*1! | 4! |
| 5! | 3!*4*5 | ||
= | = 10 | ||
| 2!*3! | 3!*2 |
| 5! | 4*5*6 | ||
= | = 30 | ||
| 2!*2! | 2*2 |
| 5! | 4!*5 | ||
= | = 5 | ||
| 4!*1! | 4! |
| 5! | 3!*4*5 | ||
= | = 10 | ||
| 2!*3! | 3!*2 |
| 5! | 4*5*6 | ||
= | |||
| 2!*2! | 2*2 |
| 5! | 2*3*4*5 | |||
źle napisałem: | = | = 30 | ||
| 2!*2! | 2*2 |