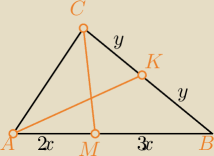
trojkacik maturzystak: zad.1 W trójkącie ABC na boku AB wybrano punkt M taki, że |AM| : |MB|=2:3. Odcinek MC dzieli środkową AK, licząc od A, w stosunku A. 2/3 B. 2/5 C. 4/15 D. 4/3

maturzystak: po rysunku widać jaka odp, ale jakby było zadanie z dowodem to nie wiedziałbym jak

===: było już n razy

maturzystak: tak widziałem, tu jest to samo zadanie, ale stosunek innego odcinka do obliczenia https://matematykaszkolna.pl/forum/256876.html tylko, że to jest dla mnie jeszcze trochę trudno do zauważenia, siedzę już trochę czasu i nie potrafię odnieść tego do drugiego odcinka..

===: zadanie jest banalne ... jeśli narysujesz przez K równoległą do AB

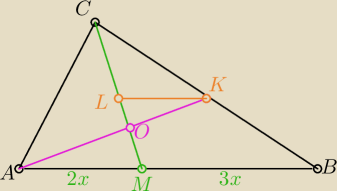
===: zaskoczyłeś? −

maturzystak: widzę, że ΔAMO jest podobny do ΔKLO (KKK) ale nadal nie do końca widzę ten stosunek AO do OK : /

Benny:

|LK|		1
	=
MB		2

	3
|LK|=		x
	2

|AM|		2x*2		4
	=		=
|LK|		3x		3

maturzystak: skad wiadomo ze |LK| / |MB| to 1/2?

maturzystak: Jak K przecina na pół odcinek CB to taka zależność jest?

Benny: LK przecina CB w połowie i jest równoległy to CM też przecina w połowie, LK musi być połową MB. Ktoś tu może wejdzie i ładnie wytłumaczy

===: ... nic dodać ... nic ując Benny a maturzystak dalej w polu i nie bardzo nawet wie co pisze Sam nie wiem skąd On to bierze ... "skąd wiadomo ze |LK| / |MB| to 1/2?"