Planimetria
Blue: Mam problem z tymi zadankami z planimetrii:
zad.1 W trójkącie ABC na boku AB wybrano punkt M taki, że |AM| : |MB|=2:3. Środkowa AK dzieli
odcinek MC, licząc od M, w stosunku:
zad.2 W trapezie ABCD, w którym AB || CD, przekątne przecinają się w punkcie O oraz
| | |DC| | |
|
| = p,p>0. Stosunek pola trapezu ABCD do pola trójkąta ABO równa się: |
| | |AB| | |
A. p
2
B. p
2+1
C. (p−1)
2
D. (p+1)
2

5 wrz 15:13
Mila:
1) Jak rozwiązujesz, nie zgadza się odp. czy nie wiesz jak wybrać?
2) Skorzystaj z podobieństwa ΔDOC i ΔAOB, PΔCOB=PΔDOA.
W razie trudności napiszę całe rozwiązanie.
5 wrz 16:50
PW: 1) A może trzeba znowu metodą eliminacji?
Na przykład rysować równoległą do AB przechodzącą przez K. Cały odcinek AK leży poniżej tej
prostej, więc L − punkt wspólny AK i CM też leży poniżej. Wobec tego
| | 1 | | 1 | |
ML : LC < |
| MC : |
| MC = 1. |
| | 2 | | 2 | |
Odpowiedź D wyeliminowana.
Dalej ni mom chęci, ale może spróbujesz?
5 wrz 18:33
Mila:
1) Najłatwiej tak, jak radzi
PW.

5 wrz 19:16
pigor: | | 2 | |
..., ...  wychodzi mi |
| , czyli odp. B |
| | 5 | |
5 wrz 20:09
Blue: Mila , nie mam pojęcia jak rozwiązać te zadania, mogłabyś napisać pełne rozwiązanie?

5 wrz 20:38
Kacper: Może ja jutro

5 wrz 21:15
Eta:
zad2/ odp D) ( tu zastosuj mój ulubiony wzorek

5 wrz 21:16
pigor: ... jak ktoś (tak, tak ...

Ciebie mam na myśli − z góry dzięki)
narysuje rysunek do zadania
1), to i ja jutro swoje rozwiązanie pokażę

5 wrz 21:25
Eta:
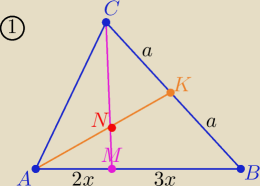
5 wrz 21:29
pigor: ..., kurde, no nie

w 4 minuty taki piękny rysunek ;
zazdroszczę Ci ; o to mi chodziło, ale do jutra; dobranoc

5 wrz 21:34
Eta:
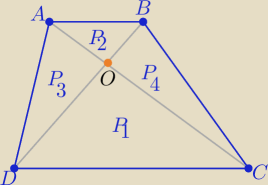
zad2/
Trójkąty DCO i ABO są podobne w skali
p
to P(ABO)=P
2 , P(DCO)= p
2*P
2 i P
3=P
4= p*P
2
P(trapezu)= P
2+2P
3+P
1 = P
2+2p*P
2+p
2*P
2= (p
2+2p+1)*P
2= (p+1)
2*P
2
P(trapezu)=
(p+1)2*P2
| P(tr) | | (p+1)2*P2 | |
| = |
| = (p+1)2 |
| P2 | | P2 | |
5 wrz 21:38
Eta:
π.. 
5 wrz 21:39
Mila:
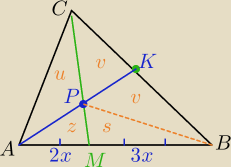
Napiszę.
1) analizujesz , trochę pomyśl, bo rozwiązanie zajmie Ci na egzaminie dużo czasu.
P− pole ΔABC
u,v,z,s − pola małych trójkątów
| | 1 | |
u+v= |
| P , bo AK to środkowa Δ |
| | 2 | |
u+v=z+s+v⇔
u=z+s
| | 2 | |
ΔAMP i ΔMPB mają wspólna wysokość⇔z= |
| s |
| | 3 | |
ΔAMP i ΔAPC mają wspólną wysokość, w takim razie
Zadanie z trapezem
Eta rozwiązywała wiele razy, wpisz Eta trapezy, znajdziesz.
5 wrz 21:39
Kacper: Zaznaczam

5 wrz 21:43
Mila:
Co zaznaczasz? Kacper?
5 wrz 21:44
Mila:
pigor, jaki masz pomysł na to zadanie (1), może krócej?
5 wrz 21:48
Eta:
Hej
Mila 
zad1/ też mam takie rozwiązanie
5 wrz 21:49
Kacper: Zaznaczam sobie, bo potem szukam zadań i znaleźć nie mogę

5 wrz 21:49
Eta:
Witam
 Kacper
Kacper .... pierwsze szlaki w szkole przetarte?
5 wrz 21:51
Mila:
Witam, Eto, moze pigor coś wymysli krótszego, błskotliwego, albo PW.
Napisałam to rozwiazanie, bo widziałam , gdzieś podobne zadanie otwarte, trzeba było obliczyc
pola wszystkich tych trójkącików.
5 wrz 21:53
pigor: ..., o

pomysł mam identyczny też z tego
tw. o stosunkach pól ΔΔ o jednakowych wysokościach
ale czy krótszy, chyba nie (mam to nabazgrane na
kartce) ; jutro zobaczę jak to wygląda

−−−−−−−−−−−−−−−−−−−−−−
a teraz idę dalej oglądać tenis ...

5 wrz 23:58
Kacper: Eta nie jest tak źle

6 wrz 07:51
Kacper:
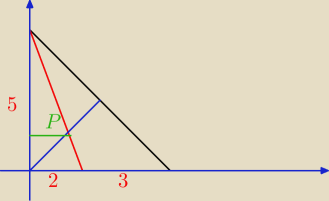
Wystarczy taki rysunek

Widać, że odp A i D odpadają (więcej niż połowa)
Zostały B i C.
Ja sobie to umieściłem w układzie współrzędnych i policzyłem współrzędne punktu P.
Nie jest to sposób uniwersalny, ale dla osób, które nie "widzą" rozwiązania
Mili wystarczą

Może jeszcze coś znajdziecie na moim rysunku, co pomoże szybciej rozwiązać

6 wrz 08:32
pigor: ..., a więc wstałem...

już, no to
(aby nie zamieszać) z rys.
Mila 21:39 i tw. o którym
mówię powyżej
zu = |MP||PC| = ? mam układ równań
dla pól powierzchni z,s,u, v ΔΔ podziału ΔABC:
z+s+v = u+v i zs = 23 ⇔ z+s = u i 3z = 2s , stąd,
szybko, bo to test np. tak:
zu +
su =1 i
su =
32*
zs ⇒
⇒
zu +
32*
zs = 1 ⇔
52*
zs =1 ⇔
zs = 25. . ...

6 wrz 08:49
Blue: Mila, a ja nawet wiem, gdzie się z podobnym zadaniem spotkałaś ^^ Dzięki wszystkim za odp!

Nie wiem, co bym bez Was zrobiła

6 wrz 09:10
Blue: Eta, nie rozumiem, jak doszłaś, że P3= p*P2.
6 wrz 09:23
5-latek: NIe rozumiem Ciebie .
czy tak trudno zajrzec do ksiazki albo wpisac w wyszukiwarke Eta trapezy
6 wrz 10:39
daras: pewnie
Blue pracuje i nie ma na to czasu, wiec wrzuca w maszynkę do rozwiazywania zadań
kolejne posty i ,cytuję: "czeka na rozwiązania"

6 wrz 10:40
Blue: A co to mi da, że tak wpiszę? Przecież tych zadań jest mnóstwo, a mi chodzi akurat o to
konkretne...
6 wrz 10:51
pigor: ...,, to może jeszcze ...

np. tak :
zad.2)
|CD| : |AB|=p ⇒
P1: P2=p2, ale P
4+P1=P
3+P1 ⇒
P4=P3 ,
ponadto P
3 : P
2 = P
1: P
3 ⇒ p
32 = P
1P
2 ⇒
P3 = √P1P2,
| | PABCD | | P1+2P3+P2 | | P3 | |
zatem |
| = |
| = p2+2 |
| +1= |
| | ΔABO | | P2 | | P2 | |
| | √P1P2 | | P1 | |
= p2+2 |
| +1= p2+2√ |
| +1= p 2+2p+1= (p+1)2...  |
| | P2 | | P2 | |
6 wrz 11:21
PW: Powróćmy do zadania 1. Banalność rozwiązania może powodować wściekłość.
Czytelnik sam sporządzi rysunek.

W podstawie trójkąta można zobaczyćć
pięć odcinków o jednakowej długości, ich końce to A,
A
1, M, B
1, B
2 i B. Prosta AK wyznacza połowę boku BC. Proste równoległe do AK przechodzące
przez A
1, M, B
1 i B
2 wyznaczają na ramieniu BC kąta ABC punkty K
1, K
2, K
3 i K
4.
Na mocy twierdzenia Talesa odcinki
KK
1, K
1K
2, K
2K
3 , K
3K
4 i K
4B
mają
także równe długości, dzielą więc odcinek KB na pięć równych części.
| | |MP| | | |K2K| | | |K2K| | | 2 | |
|
| = |
| = |
| = |
| . |
| | |PC| | | |KC| | | |KB| | | 5 | |
6 wrz 14:33
pigor: ..., No jasne,
pięknie,a przecież dobrze pamiętam tę konstrukcję
podziału odcinka jako jedno z zastosowań tw. Talesa; dziękuję
PW ; no
i teraz już wiem dlaczego to zadanie z całą odpowiedzialnością jego
autora (ów) nadaje się ...

na pewno na test ;
6 wrz 16:40
Kacper: Takie proste zadanie (o ile zna się odpowiedź)

6 wrz 17:45
PW: Biorąc pod uwagę różne padające tu pomysły i czas jaki mnie to zajęło, nie jest to takie sobie
zadanie testowe do rozwiązania w 5 minut. Co innego, jeżeli akurat "przerabiamy Talesa" −
wtedy samo się nasuwa dorysowanie czegoś równoległego.
Wniosek: zadanie dobre na klasówkę z działu "twierdzenie Talesa", na maturę już jakby mniej
dobre. Nie jest to żaden paradoks, często nadmiar wiedzy przeszkadza.

6 wrz 18:02
Kacper: Wegług mnie zadanie też na pewno nie na testowe na maturze. Jako otwarte mogłoby być.
6 wrz 18:15
Blue: Pigor, skąd się wzięło to P3 : P2 = P1: P3 ?

6 wrz 18:47
pigor: ..., no cóż niech to zostanie moją ...

"słodką" ... , bo.
i tak masz w czym wybierać, a skąd i dlaczego powinnaś już
dawno załapać, gdyż niejedno zadanie ci rozwiązałem tym
właśnie sposobem pisząc na ten temat więcej tylko, że ciebie
moje rozwiązania nie interesowały, więc niech tak zostanie .

6 wrz 19:03
Blue: To może mi powiesz chociaż skąd się wzięło P3=P4= p*P2
w rozwiązaniu Ety

?
6 wrz 19:07
Blue: I przepraszam, że być może mnie nie interesowały

Twoje rozwiązania po prostu czasem wymagają
pomyślenia, a jeśli ktoś wstawia prostszy sposób i jeszcze z rysunkiem, to sam rozumiesz

6 wrz 19:08
eta: πππ
20 paź 14:48
Eta: Δ
20 paź 14:49


 wychodzi mi
wychodzi mi 


 Ciebie mam na myśli − z góry dzięki)
narysuje rysunek do zadania 1), to i ja jutro swoje rozwiązanie pokażę
Ciebie mam na myśli − z góry dzięki)
narysuje rysunek do zadania 1), to i ja jutro swoje rozwiązanie pokażę 

 w 4 minuty taki piękny rysunek ;
zazdroszczę Ci ; o to mi chodziło, ale do jutra; dobranoc
w 4 minuty taki piękny rysunek ;
zazdroszczę Ci ; o to mi chodziło, ale do jutra; dobranoc 
 zad2/
Trójkąty DCO i ABO są podobne w skali p
to P(ABO)=P2 , P(DCO)= p2*P2 i P3=P4= p*P2
P(trapezu)= P2+2P3+P1 = P2+2p*P2+p2*P2= (p2+2p+1)*P2= (p+1)2*P2
P(trapezu)=(p+1)2*P2
zad2/
Trójkąty DCO i ABO są podobne w skali p
to P(ABO)=P2 , P(DCO)= p2*P2 i P3=P4= p*P2
P(trapezu)= P2+2P3+P1 = P2+2p*P2+p2*P2= (p2+2p+1)*P2= (p+1)2*P2
P(trapezu)=(p+1)2*P2

 Napiszę.
1) analizujesz , trochę pomyśl, bo rozwiązanie zajmie Ci na egzaminie dużo czasu.
P− pole ΔABC
u,v,z,s − pola małych trójkątów
Napiszę.
1) analizujesz , trochę pomyśl, bo rozwiązanie zajmie Ci na egzaminie dużo czasu.
P− pole ΔABC
u,v,z,s − pola małych trójkątów

 zad1/ też mam takie rozwiązanie
zad1/ też mam takie rozwiązanie

 Kacper .... pierwsze szlaki w szkole przetarte?
Kacper .... pierwsze szlaki w szkole przetarte?
 pomysł mam identyczny też z tego
tw. o stosunkach pól ΔΔ o jednakowych wysokościach
ale czy krótszy, chyba nie (mam to nabazgrane na
kartce) ; jutro zobaczę jak to wygląda
pomysł mam identyczny też z tego
tw. o stosunkach pól ΔΔ o jednakowych wysokościach
ale czy krótszy, chyba nie (mam to nabazgrane na
kartce) ; jutro zobaczę jak to wygląda  −−−−−−−−−−−−−−−−−−−−−−
a teraz idę dalej oglądać tenis ...
−−−−−−−−−−−−−−−−−−−−−−
a teraz idę dalej oglądać tenis ... 

 Wystarczy taki rysunek
Wystarczy taki rysunek  Widać, że odp A i D odpadają (więcej niż połowa)
Zostały B i C.
Ja sobie to umieściłem w układzie współrzędnych i policzyłem współrzędne punktu P.
Nie jest to sposób uniwersalny, ale dla osób, które nie "widzą" rozwiązania Mili wystarczą
Widać, że odp A i D odpadają (więcej niż połowa)
Zostały B i C.
Ja sobie to umieściłem w układzie współrzędnych i policzyłem współrzędne punktu P.
Nie jest to sposób uniwersalny, ale dla osób, które nie "widzą" rozwiązania Mili wystarczą
 Może jeszcze coś znajdziecie na moim rysunku, co pomoże szybciej rozwiązać
Może jeszcze coś znajdziecie na moim rysunku, co pomoże szybciej rozwiązać 
 już, no to
(aby nie zamieszać) z rys.Mila 21:39 i tw. o którym
mówię powyżej zu = |MP||PC| = ? mam układ równań
dla pól powierzchni z,s,u, v ΔΔ podziału ΔABC:
z+s+v = u+v i zs = 23 ⇔ z+s = u i 3z = 2s , stąd,
szybko, bo to test np. tak: zu + su =1 i su = 32*zs ⇒
⇒ zu + 32*zs = 1 ⇔ 52*zs =1 ⇔ zs = 25. . ...
już, no to
(aby nie zamieszać) z rys.Mila 21:39 i tw. o którym
mówię powyżej zu = |MP||PC| = ? mam układ równań
dla pól powierzchni z,s,u, v ΔΔ podziału ΔABC:
z+s+v = u+v i zs = 23 ⇔ z+s = u i 3z = 2s , stąd,
szybko, bo to test np. tak: zu + su =1 i su = 32*zs ⇒
⇒ zu + 32*zs = 1 ⇔ 52*zs =1 ⇔ zs = 25. . ...
 Nie wiem, co bym bez Was zrobiła
Nie wiem, co bym bez Was zrobiła 

 np. tak : zad.2)
|CD| : |AB|=p ⇒ P1: P2=p2, ale P4+P1=P3+P1 ⇒ P4=P3 ,
ponadto P3 : P2 = P1: P3 ⇒ p32 = P1P2 ⇒ P3 = √P1P2,
np. tak : zad.2)
|CD| : |AB|=p ⇒ P1: P2=p2, ale P4+P1=P3+P1 ⇒ P4=P3 ,
ponadto P3 : P2 = P1: P3 ⇒ p32 = P1P2 ⇒ P3 = √P1P2,

 W podstawie trójkąta można zobaczyćć pięć odcinków o jednakowej długości, ich końce to A,
A1, M, B1, B2 i B. Prosta AK wyznacza połowę boku BC. Proste równoległe do AK przechodzące
przez A1, M, B1 i B2 wyznaczają na ramieniu BC kąta ABC punkty K1, K2, K3 i K4.
Na mocy twierdzenia Talesa odcinki
KK1, K1K2, K2K3 , K3K4 i K4B
mają także równe długości, dzielą więc odcinek KB na pięć równych części.
W podstawie trójkąta można zobaczyćć pięć odcinków o jednakowej długości, ich końce to A,
A1, M, B1, B2 i B. Prosta AK wyznacza połowę boku BC. Proste równoległe do AK przechodzące
przez A1, M, B1 i B2 wyznaczają na ramieniu BC kąta ABC punkty K1, K2, K3 i K4.
Na mocy twierdzenia Talesa odcinki
KK1, K1K2, K2K3 , K3K4 i K4B
mają także równe długości, dzielą więc odcinek KB na pięć równych części.
 na pewno na test ;
na pewno na test ;



 "słodką" ... , bo.
i tak masz w czym wybierać, a skąd i dlaczego powinnaś już
dawno załapać, gdyż niejedno zadanie ci rozwiązałem tym
właśnie sposobem pisząc na ten temat więcej tylko, że ciebie
moje rozwiązania nie interesowały, więc niech tak zostanie .
"słodką" ... , bo.
i tak masz w czym wybierać, a skąd i dlaczego powinnaś już
dawno załapać, gdyż niejedno zadanie ci rozwiązałem tym
właśnie sposobem pisząc na ten temat więcej tylko, że ciebie
moje rozwiązania nie interesowały, więc niech tak zostanie .
 ?
?
 Twoje rozwiązania po prostu czasem wymagają
pomyślenia, a jeśli ktoś wstawia prostszy sposób i jeszcze z rysunkiem, to sam rozumiesz
Twoje rozwiązania po prostu czasem wymagają
pomyślenia, a jeśli ktoś wstawia prostszy sposób i jeszcze z rysunkiem, to sam rozumiesz 