aa
Hugo: Zadanie 4. Niech S będzie zbiorem wszystkich ciągów o długości dziesięć złożonych
z cyfr 0,1,2.
(a) Ile elementów ma zbiór S?
(b) Ile ciągów należących do S ma dokładnie 5 jedynek i 5 zer?
(c) Ile ciągów należących do S ma dokładnie 3 jedynki i 7 zer?
(d) Ile ciągów należących do S ma dokładnie 3 zera i 4 jedynki i 3
dwójki?
(e) Ile ciągów należących do S ma co najmniej 1 zero co najmniej 1
jedynke i co najmniej 1 dwójkę
a) czyli:
0 1 2 10 11 12 20 21 22 100 ..............101 102 110 111 112 120

21 kwi 15:50
Jacek: a)
np. 0012001022 − jeden ciąg o długości dziesięć złożony z cyfr 0,1,2
21 kwi 16:06
Jacek: w związku z tym, że nie ma ograniczenia, iż muszą to być liczby, to dopuszczamy 0 na czele, tak
mi się wydaje
21 kwi 16:07
Hugo: Racja

bo to jest CIąg liczb wszystkich 10cyfrowych
21 kwi 16:08
Jacek: a)
Wszystkich takich ciągów jest:
310
, więc S właśnie tyle ma elementów.
Odczytuje to tak, że długość dziesięć dotyczy ciągów, a nie jest długością zbioru S,
czymkolwiek by to było.
21 kwi 16:10
Hugo:
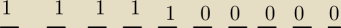
Czyli a)
3
9 * 2

bo na 1 miejscu nie moze byc zera !
b)
Ile ciągów należących do S ma dokładnie 5 jedynek i 5 zer? czyl dwójek nie ma

i ona mogą
wokół siebie wariować tylko jak to wyliczyć ;−; ?!
21 kwi 16:10
Hugo: Dobrze myśle

? 16:10
21 kwi 16:11
Jacek: Nie widzę w treści zadania, że mają to być liczby. W związku z tym chyba nie możemy pominąć
takich ciągów jak np.
0 0 2 0 0 1 2 0 1 1
21 kwi 16:16
Hugo: Mnie kusi dwumian Netwona

C
510 * C
55 ale no

?
21 kwi 16:16
Hugo: 
ok czyli 3
10 !
b) dobrze mysle?
21 kwi 16:17
Hugo: (c) Ile ciągów należących do S ma dokładnie 3 jedynki i 7 zer?
3 jedynki i 7 zer
C
310 * C
710


21 kwi 16:22
Hugo: (d) Ile ciągów należących do S ma dokładnie 3 zera i 4 jedynki i 3
dwójki?
czyli

C
310 * C
47 * C
33 i tu mnożymy razy 3! bo rozróżniamy te ciągi nie

?
21 kwi 16:24
21 kwi 16:25
21 kwi 16:26
21 kwi 16:27
Hugo:
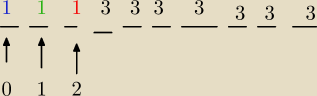
(e) Ile ciągów należących do S ma co najmniej 1 zero co najmniej 1
jedynke i co najmniej 1 dwójkę
1*1*1* 3
7 
?
21 kwi 16:30
Hugo: @Jacek a nie mnożymy w ponpunkcie d) przez 3 !

nie rozróżniamy tego?
21 kwi 16:31
Hugo: Zadanie 5.
Na ile różnych sposobów można podzielić 19 studentów na 5 zespołów
w tym 2 zespoły po 5 osób i 3 zespoły po 3 osoby tak aby
(a) każdy zespół studiował inny spośród 5 danych tematów
(b) każdy zespół studiuje ten sam temat
Czyli Kombinacje

!
| | | | | | | | | | | |
a) | * | * | * | * | i tu rozróżniamy * 5! |
| | | | | | |
21 kwi 16:37
Jacek: Pewnie się odnosisz do tego nocnego zadania z komisjami.
Tu nie jest tak.
Mamy na sztywno przypisaną ilość wyborów z danego zbioru np. 3 razy 0, tam istniała możliwość,
że komisja nr 1 będzie mogła liczyć 3 lub 4 lub 5.
Poza tym tu, nawet jeśli byłaby taka dowolność, możliwe układy wyboru liczebności pod dane
zbiory wyglądałyby tak:
3+4+3
3+3+4
4+3+3
, czyli takich układów byłoby: 3
Byśmy mieli wówczas:
Polecam, choć nie do końca podobne
https://matematykaszkolna.pl/forum/285288.html , szczególnie wpis
PW
21 kwi 16:43
Hugo: Zadanie 6. Na ile sposobów można podzielić zbiór złożony z 2n elementów na dwa
zbiory po n elementów w każdym?
| |
* n !  bo elementy mogą być różne wybieramy dwa n−elementowe z 2n−elementowego i |
| |
razy 5! (6*4*5) rozróżnień bo wierzymy ze elementy są różne

a tamto miales racje ze bez silni zad 4c)

!
21 kwi 16:43
21 kwi 16:45
Jacek: zasadniczo, nie chodzi o rozróżnialność, bo tę z góry chyba należy zakładać za obecną w
zadaniu...
21 kwi 16:49
Hugo: 
ok
21 kwi 16:59
Jacek: Tak, szczerze to walisz zadaniami, które dla mnie są z reguły na poziomie co najmniej
zaawansowanym, także nie jestem specjalnie przekonany co do odpowiedzi.
21 kwi 17:02
Hugo: Zadanie 7. Worek zawiera 50 szklanych kulek w 4 różnych kolorach. Wyjaśnij
dlaczego jest co najmniej 13 kulek tego samego koloru.

dyfuzja ciał stałych pod wpływem czasu !
Gdyś 50/4 kolory(gdyby po równo) = 12,5 ale z uwagi że kulek nie dzielimy to dwa kolory będą
mieć o jedną kulke więcej

czyli 13 !
21 kwi 17:02
Hugo: @Jacek: Ja zauważam że tu wszędzie wszystko opiera się na KOMBINACJACH

i nie ma specjalnie
jakiś trudnych, zależy mi na wykryciu głupich błędów... Za zadania nic nie dostane, troche
wiedzy i może sie uda aktywnośc coś

walcze o 4,0 z DYSKRETNEJ !
Dziękuję Ci za wszelaki czas tu spędzony
21 kwi 17:04
Hugo: 
7 zadan na 13 mam myśle ze styknie

i tak reszta to juz na logike idzie
Dziękuje wielkie !
21 kwi 17:20
Jacek: Nie chcę Ciebie zniechęcać, ale nie sądzę, by to było takie proste...na razie to myślę nad
piątym zadaniem.
21 kwi 17:23
Jacek: Bo tu nie dość, że ludzi przyporządkowujemy do zespołów, to jeszcze jest jakiś wybór dla
zespołu tematu.
21 kwi 17:26
Hugo: : > uu
21 kwi 18:05
Jacek: Wiesz co, zacznijmy od zmodyfikowania zadania, tak by dostrzec co gdzie i kiedy.
Mamy 5 studentów, dzielimy na dwa zespoły 2 + 3 osobowe. Na ile różnych sposobów można
podzielić te osoby?
Kluczowe jest to co jest wynikiem.
Dla mnie dobrym modelem jest gdy danej osobie przyporządkowujemy numer zespołu.
Mamy wtedy wynik takiego doświadczenia losowego:
− oznaczmy numery zespołów cyframi: 1, 2
Pierwsza cyfra w takim ciągu jest przyporządkowana zawsze pierwszej osobie, druga cyfra drugiej
osobie itd. Z tego co zauważyłem, praktycznie w 100% nie jest ważne jako która dana np. osoba
losuje sobie numer grupy.
Otrzymujemy następujące wariacje w wyniku działania (nie myśl, że w wyniku mnożenia kombinacji
zawsze otrzymasz kombinacje

):
Dla układu:
3x "nr 1" + 2x "nr 2"
1 1 1 2 2
1 1 2 1 2
1 1 2 2 1
1 2 1 2 1
1 2 1 1 2
1 2 2 1 1
2 1 1 1 2
2 1 1 2 1
2 1 2 1 1
2 2 1 1 1
Dla układu:
2x "nr 1" + 3x "nr 2"
2 2 2 1 1
2 2 1 2 1
2 2 1 1 2
2 1 2 1 2
2 1 2 2 1
2 1 1 2 2
1 2 2 2 1
1 2 2 1 2
1 2 1 2 2
1 1 2 2 2
Ostatecznie zapisałbym:
I teraz tak:
− Jeżeli zadanie byłoby sformułowane tak, że Zespół nr 1 ma liczyć trzy osoby, Zespół nr 2 dwie
osoby, to:
− Jeżeli numery zespołów nie mają znaczenia, a dalej dopytują się na ile sposobów można
podzielić te pięć osób, to robi się ciekawie, bo wówczas liczą się liczy się tylko ile jest
wariacji, gdzie np. dane trzy osoby znajdą się w jednym zespole.
Wówczas układy:
1 1 1 2 2 jest tak samo liczony jak 2 2 2 1 1
I to jest dopiero początek zabawy, bo czasem takie zadania mają wyższy stopień skomplikowania
np.
− nie wszystkie osoby wchodzą w skład dokonujących wyboru, skład dokonujący wyboru jest losowo
zawężany
− nie wszystkie numery zespołów muszą być wykorzystane, też mogą być losowo zawężane podzbiory
z tymi numerami
− no i tak jak u Ciebie dochodzi jeszcze przyporządkowanie, gdzie już danemu zespołowi w danym
składzie osobowym, przypisywany jest temat

21 kwi 19:39
Jacek: miałem napisać:
Wówczas układy
11122 jest tożsamy 22211
21 kwi 19:40
Jacek: Jeszcze "piękniej" wygląda sytuacja, gdy numery zespołów się nie liczą, a ilość osób w każdym z
zespołów jest taka sama. Np. 4 osoby, dwa zespoły 2 dwu−osobowe.
1 1 2 2
1 2 1 2
1 2 2 1
2 2 1 1
2 1 2 1
2 1 1 2
, tylko że 1 1 2 2 jest tożsame 2 2 1 1
1 2 1 2 jest tożsame 2 1 2 1
etc.
I będzie takich sposobów, w których wybór numeru zespołu nie ma znaczenia:
21 kwi 20:55

 bo to jest CIąg liczb wszystkich 10cyfrowych
bo to jest CIąg liczb wszystkich 10cyfrowych
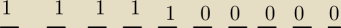 Czyli a)
39 * 2
Czyli a)
39 * 2  bo na 1 miejscu nie moze byc zera !
b)
Ile ciągów należących do S ma dokładnie 5 jedynek i 5 zer? czyl dwójek nie ma
bo na 1 miejscu nie moze byc zera !
b)
Ile ciągów należących do S ma dokładnie 5 jedynek i 5 zer? czyl dwójek nie ma  i ona mogą
wokół siebie wariować tylko jak to wyliczyć ;−; ?!
i ona mogą
wokół siebie wariować tylko jak to wyliczyć ;−; ?!
 ? 16:10
? 16:10
 C510 * C55 ale no
C510 * C55 ale no ?
?
 ok czyli 310 !
b) dobrze mysle?
ok czyli 310 !
b) dobrze mysle?


 C310 * C47 * C33 i tu mnożymy razy 3! bo rozróżniamy te ciągi nie
C310 * C47 * C33 i tu mnożymy razy 3! bo rozróżniamy te ciągi nie  ?
?



 a d)?
a d)?
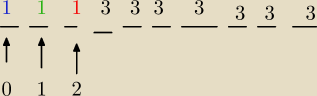 (e) Ile ciągów należących do S ma co najmniej 1 zero co najmniej 1
jedynke i co najmniej 1 dwójkę
1*1*1* 37
(e) Ile ciągów należących do S ma co najmniej 1 zero co najmniej 1
jedynke i co najmniej 1 dwójkę
1*1*1* 37  ?
?
 nie rozróżniamy tego?
nie rozróżniamy tego?
 !
!
 bo elementy mogą być różne wybieramy dwa n−elementowe z 2n−elementowego i
bo elementy mogą być różne wybieramy dwa n−elementowe z 2n−elementowego i a tamto miales racje ze bez silni zad 4c)
a tamto miales racje ze bez silni zad 4c)  !
!
 tez wlasnie cos myślałem ze jednak tak ma byc potem !
Jak reszta zadań
tez wlasnie cos myślałem ze jednak tak ma byc potem !
Jak reszta zadań ?
mam ich 13
?
mam ich 13  http://wms.mat.agh.edu.pl/~dudekane/zestaw8.pdf
http://wms.mat.agh.edu.pl/~dudekane/zestaw8.pdf
 ok
ok
 dyfuzja ciał stałych pod wpływem czasu !
Gdyś 50/4 kolory(gdyby po równo) = 12,5 ale z uwagi że kulek nie dzielimy to dwa kolory będą
mieć o jedną kulke więcej
dyfuzja ciał stałych pod wpływem czasu !
Gdyś 50/4 kolory(gdyby po równo) = 12,5 ale z uwagi że kulek nie dzielimy to dwa kolory będą
mieć o jedną kulke więcej  czyli 13 !
czyli 13 !
 i nie ma specjalnie
jakiś trudnych, zależy mi na wykryciu głupich błędów... Za zadania nic nie dostane, troche
wiedzy i może sie uda aktywnośc coś
i nie ma specjalnie
jakiś trudnych, zależy mi na wykryciu głupich błędów... Za zadania nic nie dostane, troche
wiedzy i może sie uda aktywnośc coś  walcze o 4,0 z DYSKRETNEJ !
Dziękuję Ci za wszelaki czas tu spędzony
walcze o 4,0 z DYSKRETNEJ !
Dziękuję Ci za wszelaki czas tu spędzony
 7 zadan na 13 mam myśle ze styknie
7 zadan na 13 mam myśle ze styknie  i tak reszta to juz na logike idzie
Dziękuje wielkie !
i tak reszta to juz na logike idzie
Dziękuje wielkie !
 ):
Dla układu:
3x "nr 1" + 2x "nr 2"
):
Dla układu:
3x "nr 1" + 2x "nr 2"
