granica ciągu Adamxd: Czy ktoś mógłby wytłumaczyc mi słowa pana z tego filmu ze jesli 1 podzielimy przez nieskoczonosc to otrzymamy zero − ja bym tutaj polemizował... https://www.youtube.com/watch?v=xuYqwwTmVeI&index=2&list=PL797C7389C3FF6B5F

Ajtek: Dlaczego byś polemizował?

Adamxd: no bo jak 1 przez cos nieskonczonego moze = 0 − wytlumacz to ktos...

Adamxd:

/_/_/\_\/_/\_\/_/\_\_\: A gdybyś np. miał przejść drogę równą 100km i każdego dnia przechodził połowę tej drogi to jak

	100		100		100		100
wyglądała by dorga przebyta w następnych dniach?						..
	2		4		16		8192

do czego zmierzają te liczby?

Adamxd: do zera ale nigdy go nie osiagna wiec dlatego upieram sie ze 1 przez nieskonczonosc ≠ 0

5-latek:

a
	=0 gdzie a to stala
∞

A jeśli chcesz się upierac twoje prawo ale zaliczenia z granic funkcji czy ciagow nie dostaniesz

5-latek: Tak samo jak mogloby się wydawac ze ∞ −∞=0 ale to nieprawda (nie wiadomo do czego to dazy

Saizou : ciąg a_n ma granicę niewłaściwą w +∞ jeśli dla każdego M∊R istnieje n_o takie że dla każdego n>n₀ zachodzi a_n>M

Saizou : o Jezu... o czym innym pomyślałem xd

Adamxd: ok, zapamietam ta stala − nie moge sb pozwolic na ocene zawierającą się w przedziale <1,5)

Saizou :

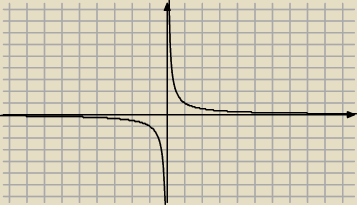
1		1
	→0 przy x→∞, tylko się zwykło pisać że		=0 przy x→∞
x		x

PW: A tak w ogóle to nie słuchaj tego pana, jeżeli rzeczywiście powiedział to co cytujesz. Powiedzenie, że "1 podzielone przez nieskończoność jest równe 0" to brednia.

Adamxd: to juz podchodzi pod filozofie...

Adamxd: no ale jak obliczal granice na tym filmie to korzystal z tego ze 1 przez ∞ = 0

Saizou : Cytuję: "Jeżeli jedynkę podzielmy przez coś nieskończenie dużego, no to oczywiście otrzymamy zero"

PW: Nie będę oglądał filmików. Nieskończoność nie jest liczbą. Nie można podzielić 1 przez krzesło, bo krzesło nie jest liczbą, Tak samo z nieskończonością. Poprawny komentarz to powołanie się na twierdzenie o granicy ilorazu dwóch ciągów, z których jeden dąży do nieskończoności, a drugi ma granicę skończoną. Nie cytuję dokładnie, by zachęcić Cię do znalezienia tego twierdzenia zamiast powtarzania "popularnych wersji twierdzeń, których nikt nie zna".

PW: Nawet jeżeli ten pan powiedział to co cytuje Saizou, to i tak bardziej szkodzi niż pomaga.

Adamxd: No to dlaczego przy obliczaniu granic on traktuje to wyrażenie jako zero

PW: A Ty swoje. Znajdź twierdzenie, o którym piszę o 22:08. Ucz się z podręczników, a nie z popularnych opowiastek, bo zamiast wiedzieć co liczysz, nauczysz się co najwyżej "jak to się robi".

maturzysta: https://matematykaszkolna.pl/forum/290041.html ktoś pomoże ?

sadas: @Adamxd bo jesteś idiotą.