Bogdan:
Można przeprowadzić następujące rozumowanie:
Jeśli równanie miałoby dwa różne pierwiastki, to jeden z nich byłby podwójnym pierwiastkiem,
oznaczmy je następująco: x
1 = x
2 = a, x
3 = b.
Postać iloczynowa w takim przypadku ma postać: (x − a)
2(x − b) = 0. Po wymnożeniu
otrzymujemy: x
3 + (−2a − b)x
2 + (2ab + a
2)x − a
2b.
Porównując współczynniki mamy: −2a − b = 0 ⇒ b = −2a, m = −a
2 − 2ab = 3a
2,
−a
2b = 2 ⇒ 2a
3 = 2 ⇒ a = 1. Stąd m = 3
Podane równanie x
3 − mx + 2 = 0 można zapisać: x
3 = mx − 2
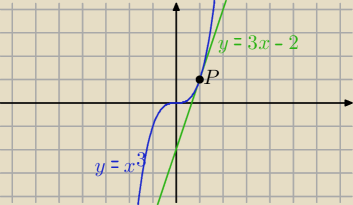
Prosta y = 3x − 2 jest styczną do krzywej y = x
3 w punkcie P(1, 1). Biorąc współczynnik
kierunkowy tej prostej w zakresie (3, +
∞) otrzymujemy sieczną tej krzywej mającą z nią
3 punkty wspólne.
Ostatecznie równanie x
3 − mx + 2 = 0 ma trzy rozwiązania dla m∊(3, +
∞)
 Można przeprowadzić następujące rozumowanie:
Jeśli równanie miałoby dwa różne pierwiastki, to jeden z nich byłby podwójnym pierwiastkiem,
oznaczmy je następująco: x1 = x2 = a, x3 = b.
Postać iloczynowa w takim przypadku ma postać: (x − a)2(x − b) = 0. Po wymnożeniu
otrzymujemy: x3 + (−2a − b)x2 + (2ab + a2)x − a2b.
Porównując współczynniki mamy: −2a − b = 0 ⇒ b = −2a, m = −a2 − 2ab = 3a2,
−a2b = 2 ⇒ 2a3 = 2 ⇒ a = 1. Stąd m = 3
Podane równanie x3 − mx + 2 = 0 można zapisać: x3 = mx − 2
Prosta y = 3x − 2 jest styczną do krzywej y = x3 w punkcie P(1, 1). Biorąc współczynnik
kierunkowy tej prostej w zakresie (3, +∞) otrzymujemy sieczną tej krzywej mającą z nią
3 punkty wspólne.
Ostatecznie równanie x3 − mx + 2 = 0 ma trzy rozwiązania dla m∊(3, +∞)
Można przeprowadzić następujące rozumowanie:
Jeśli równanie miałoby dwa różne pierwiastki, to jeden z nich byłby podwójnym pierwiastkiem,
oznaczmy je następująco: x1 = x2 = a, x3 = b.
Postać iloczynowa w takim przypadku ma postać: (x − a)2(x − b) = 0. Po wymnożeniu
otrzymujemy: x3 + (−2a − b)x2 + (2ab + a2)x − a2b.
Porównując współczynniki mamy: −2a − b = 0 ⇒ b = −2a, m = −a2 − 2ab = 3a2,
−a2b = 2 ⇒ 2a3 = 2 ⇒ a = 1. Stąd m = 3
Podane równanie x3 − mx + 2 = 0 można zapisać: x3 = mx − 2
Prosta y = 3x − 2 jest styczną do krzywej y = x3 w punkcie P(1, 1). Biorąc współczynnik
kierunkowy tej prostej w zakresie (3, +∞) otrzymujemy sieczną tej krzywej mającą z nią
3 punkty wspólne.
Ostatecznie równanie x3 − mx + 2 = 0 ma trzy rozwiązania dla m∊(3, +∞)