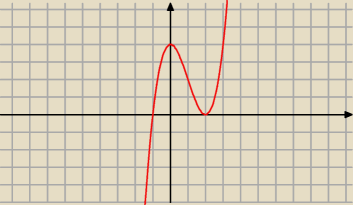
maturalne zadania z pochodnymi YushokU: Witam, Mam kłopot z dwoma zadankami. Zad.1 Wyznacz wszystkie wartości parametru m, dla których równanie x³−mx+2=0 ma trzy rozwiązania. Założenia: f_max≥0 f_min≤0 f_min≠f_max f(x)=x³−mx+2 f'(x)=3x²−m

	−m√3		m√3
f'(x)=0 dla m∊{		},		}
	3		3

	m√3		√3m3		m2√3
fmin=f(		)=		−		+2
	3		9		3

	−m√3		−√3m3		m2√3
fmax=f(		)=		+		+2
	3		9		3

f_min≤0

√3m3		m2√3
	−		+2≤0
9		3

i teraz po wymnożeniu przez 3√3 m³−3m²+6√3≤0 podobnie z f_max≥0 −m³+3m²+6√3≤0 No i teraz ani nie widzę tu pierwiastka, rachunki posprawdzane, nie wiem co z tym zrobić. Wiem, że tu się kryje rozwiązanie, ale nie umiem do tego dotrzeć. Zad.2 Pole podstawy stożka, pole powierzchni kuli wpisanej w ten stożek oraz pole powierzchni bocznej stożka tworzą, w podanej kolejności ciąg arytmetyczny. Oblicz cosinus kąta nachylenia tworzącej stożka do płaszczyzny jego podstawy Tutaj propozycję rozwiązania zadania umieszczę pod tym postem, żeby zrobić rysunek ładnie.

b.: pomyłka w 1.: pierwiastkami pochodnej są x = +− √m3{3}, tzn. m też jest pod pierwiastkiem

b.:

	√3m
x=+−
	3

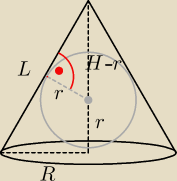
YushokU: R−promień podstawy stożka r−promień kuli L−tworząca stożka P_p=πR² P_k=4πr² P_b=πRL L>R>0 Teraz z warunki istnienia ciągu arytmetycznego. 2b=a+c 8r²=R²+RL L²−R²=H²

r		R
	=
√L2−R2−r		L

po obliczeniu.

	R(L−R)
r2=
	L+R

podstawiam do równania z warunkiem istnienia ciągu

	R(L−R)
8		=R(R+L)
	L+R

Otrzymuję równanie. R²+R(2L+8)+L²−8L=0 √Δ=8√L+1 Rozwiązanie należące do dziedziny to R=4√L+1−L−4 Myślałem, że idąć tą drogą otrzymam coś ładnego, z czego wyliczę cosinus, ale teraz, to nie wiem już co robić Jak rozwiązać te zadania? Do ZAD.1 odpowiedź to m∊(3,+∞) A do ZAD.2 odpowiedź to cos=U{1}[3} Proszę o pomoc i z góry za nią dziękuję

YushokU: Zad.1 ajjj. ale to otrzymuję jeszcze gorszy bałagan niż miałem ale spróbuję policzyć teraz

YushokU: Wychodzi. Super Ale straciłem przez ten głupi tyle czasu...

YushokU: Jakby ktoś jeszcze na drugie znalazł ochotę i chwilkę czasu to będę baaaardzo wdzięczny A i zapomniałem. @b − dziękuję !

YushokU: A jednak 1 nie do konca wychodzi. Otrzymuję przedział <3,+∞) a nie (3,+∞), ponieważ f_min=f{max} zachodzi dla tylko x=0. Czyli czegoś nie uwzględniłem. Ktoś widzi czego brakuje?

YushokU: up!

b.: Właściwie powinieneś rozważać f_min<0 i f_max>0, bo w przypadku równości mamy pierwiastek podwójny, czyli tylko 2 różne rozwiązania.

YushokU: aaaa fakt Ale jestem głupi... To jeszcze przypominam, że zadanie 2 chciałoby zostać rozwiązane

Mila: 2) wg Twoich oznaczeń.

	R
cosα=
	L

======== 8πr²=πR²+πR*L z wł. ciągu arymetycznego⇔ (*) 8r²=R²+R*L Z podobieństwa Δ:

R		r
	=		stąd: ( sprawdź !)
L		H−r

	R*H
r=		/2⇔
	L+R

	R2*H2		R2*(L2−R2)
r2=		⇔r2=		⇔
	(L+R)2		(L+R)2

	R2*(L−R)*(L+R)
r2=
	(L+R)2

	R2(L−R)
r2=
	(L+R)

Podstawiam do lewej strony (*)⇔

8*R2(L−R)		8*R2(L−R)
	=R2+R*L⇔		=R*(R+L)⇔
(L+R)		(L+R)

8R*(L−R)=(R+L)² 8R*L−8R²=R²+2R*L+L²⇔ 9R²−6R*L+L²=0⇔ (3R−L)²=0 L=3R

	R
cosα=
	3R

	1
cosα=
	3

================

YushokU: hmmm... Widzę błąd. Ale głupio. Mila przepraszam za twoją stratę czasu, no i dziękuję jednocześnie. Nawet nie wiem jak mi się to udało schrzanić, przecież już tyle zadań z tym podobieństwem robiłem

b.: A jeśli chodzi o to, gdzie u Ciebie jest błąd, to w linijce w której wyliczasz r² powinno być R² po prawej. Tutaj ten błąd można dość łatwo znaleźć patrząc na jednostki: lewa strona ma jednostkę, powiedzmy, [m²], a prawa [m], więc brakuje jakiegoś czynnika po prawej. (Nie w każdym zadaniu tak jest, tutaj były wszystkie długości oznaczone przez H,L,R,r, więc potem można porównywać jednostki po obu stronach, gdy w zadaniu jest np. podane, że jakaś długość wynosi 2, to po skorzystaniu z tego już nie można porównywać jednostek po obu stronach).

YushokU: Aha, faktycznie. Będę teraz zwracał na to uwagę, będzie mi łatwiej znaleźć błąd