Optymalizacja Robercik112: Optymalizacja ! Ważne Na wykresie funkcji y=1/4x⁴−x³−5x²+22x+50 znajdz współrzędne punktu A, którego odległość od prostej o równaniu y=−2x−22 jest najmniejsza.

===: ... tak nie możesz pisać 1/4x²

Robercik112: ?

===: tu masz podobne zadanie (zad.3.) https://matematykaszkolna.pl/forum/289571.html

===:

	1
(1/4)x4 albo x4/4 albo		x4
	4

	1
To co zapisałeś należy odczytać jako
	4x4

Robercik112: ¹₄x²

Robercik112: ¹₄x⁴

Robercik112: te zadanko co pokazales to identyko wielkie dzięki

Robercik112: tylko mam problem z wyznaczeniem tych miejsc zerowych

Robercik112: I problem polega na tym ze te miejsca zerowe nie bede liczbami calkowitymi tylko ~1,81 itp

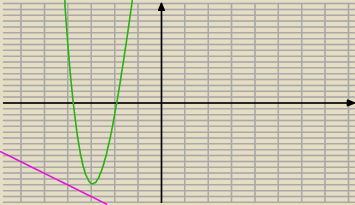
===: a co Cię interesują miejsca zerowe ? Popatrz raz jeszcze na metodę podaną w linku jeśli f(x)=x⁴/4−x³−5x²+22x+50 to f'(x)=x³−3x²−10x+22 Szukamy punktów w których styczna do f(x) jest równoległa do y=−2x−22 zatem: x³−3x²−10x+22=−2 x³−3x²−10x+24=0 x₁=−3 x₂=2 x₃=4 Są to iks−owe współrzędne punktów leżących na f(x) w których styczna do wykresu jest równoległa do y=−2x−22 Współrzędne y−kowe znajdziesz równania f(x) f(−3)= f(2)= f(4)= itd −

Robercik112: według mnie te współrzędne to (−16,−3) dobrze mysle?

===: ... niestety ... chyba nie myślisz −:(

Robercik112: dobra chyba wiem

Robercik112: dobra jednak nie

Robercik112: Obliczylem te wspołrzedne ykowe i potem policzylem od tych wspolrzednych co mi wyszly odleglosci do prostej w takim razie co zle robie?

Robercik112: Dobra mam (−3,−16)

Robercik112: ?

Robercik112: Dobra Ostateczna odpowiedz (−3,−⁵⁵₄)