Kilka zadań z rachunku różnickowego. Blue:

	1
zad.1 Prosta o równaniu y=		x jest styczna do wykresu funkcji :
	4

	x2−x		1
f(x) =		+cos2α −		sinα w punkcie o dodatniej odciętej. Wyznacz α, jeśli
	3x+1		2

α∊<0,π>. zad.2 Uzasadnij, że funkcja f nie ma pochodnej w punkcie x=0.

	8x
f(x) = |		|
	x2+1

zad.3 Wyznacz współrzędne punktu P należącego do wykresu funkcji f i leżącego najbliżej prostej x−y+2=0.

	2x−3
f(x) =		.
	x−1

zad.4 Wyznacz dziedzinę funkcji f, określ jej najmniejszą wartość oraz naszkicuj wykres, jeśli f(x) = lim(1+x²+x⁴+...+x²ⁿ) x−>∞

===: 1) Proponuję tak: −liczysz pochodną f'(x) −przyrównujesz do 1/4 w ten sposób wyznaczysz współrzędną punktu/punktów styczności drugie współrzędne wyznaczysz podstawiając do równania prostej −współrzędne punktów styczności podstawiasz do f(x) w ten sposób wyznaczysz wartości α

Blue: Wyszło ! Dzięki wielkie, na początku nie wiedziałam jak w ogóle się za to wziąć, bo widziałam dwie niewiadome, ale przecież jak obliczymy pochodną, to te wszystkie f. trygonometryczne znikną ^^

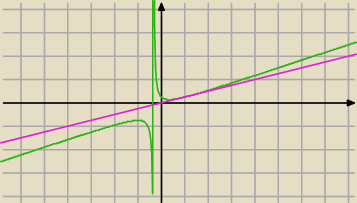
===: 1)

	(2x−1)(3x+1)−3(x2−x)		3x2+2x−1
f'(x)=		=
	(3x+1)2		(3x+1)2

f'(x)=1/4 zatem: 12x²+8x−4=9x²+6x+1 ⇒ 3x²+2x−5=0 Δ=64 x₀₁=1 x₀₂=−5/3 do y=x/4 zatem: y{01)=1/4 y₀₂=−5/12 Wcześniej uporządkujmy cos2α−0,5sinα=1−sin²α−0,5sinα=−2sin²α−0,5sinα+1 i teraz

1		1−1
	=		−2sin2α−0,5sinα+1 ⇒ −8sin2α−2sinα+3=0
4		3+1

	2+10
Δ=4+96=100 sinα=		po za przedziałem
	−16

	2−10
lub sinx=		=0,5 α=...
	−16

Dla porządku sprawdzę na wykresie Drugi punkt styczności już dla Ciebie −

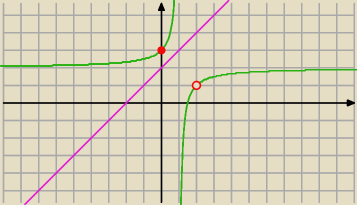
===: to pobawię się jeszcze 3)

	2x−3
f(x)=		i prosta y=x+2
	x−1

Można odległością punktu od prostej i szukanie minimum ale ja jestem za leniwy− dlatego poszukam punktów w których styczna do f(x) jest równoległa do danej prostej.

	2(x−1)−2x+3		1
f'(x)=		=
	(x−1)2		(x−1)2

f'(x)=1 x(x−2)=0 x₁=0 lub x₂=2 drugie współrzędne wyznaczysz z równania f(x) zatem: y₁=3 y₂=1 Pozostaje Ci policzyć, który z tych punktów leży bliżej danej prostej −

Mila: Ładny sposób.

===: −

Blue: Drugiego punktu nie trzeba rozpatrywać, bo odcięta ma być dodatnia Dziękuję też za rozwiązanie 3, właśnie ja próbowałam liczyć z odległości punktu od prostej i z pochodnej, ale coś nie wychodziło... Ktoś się pokusi o zrobienie 2 i 4

Mila: Zadanie 2 .

	−8x
f(x)=		dla x<0
	x2+1

	8x
f(x)=		dla x≥0 i licz granicę ilorazu różnicowego.
	x2+1

Blue: czyli w jednym przypadku będzie −8, a w drugim 8

Mila: Liczysz granicę ilorazu różnicowego w x₀=0

Blue: Mila, a mogłabyś to rozpisać?

Blue:

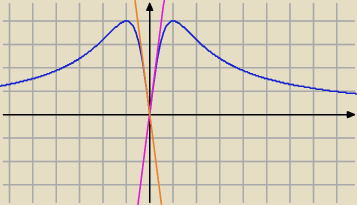
Mila: Przedtem zgubiłam 8 w liczniku, nie popatrzyłam uważnie na wzór, przepraszam.

	8|0+h|   −0 (0+h)2+1		8*(−h)
limh→0−		=limh→0−		=−8
	h		h*(h2+1)

Dalej dla h→0⁺

	8|0+h|   −0 (0+h)2+1		8*(h)
limh→0+		=limh→0+		=8
	h		h*(h2+1)

Blue: Czyli jednak mam dobrze Dziękuję A pomogłabyś mi jeszcze z 4? Przepraszam, że Cię męczę (: