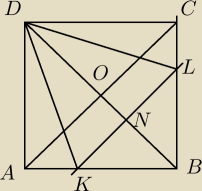
Trójkąt wpisany w kwadrat Bronek: Pomóżcie: |AD|=|AB|=|BC|=|CD|=a; |DK|=|DL|; |ON|=b Dane;a,b Policz tg∡KDL

Jacek:

	a√2
|NB|=		−b
	2

∡KNB=90^o ∡KBN=45^o, bo rozpatrujemy kwadrat , zatem: |KN|=tg∡KBN *|NB|

	|KN|
tg∡KDN=
	|DN|

	2*tg∡KDN
tg∡KDL=
	1−tg2∡KDN

Bronek: ? ? ?

Jacek: ∡KDL=2*∡KDN, bo trójkąt jest równoramienny, skoro |DK|=|DL| , zatem mając tg∡KDN musimy policzyć tg kąta 2 razy większego. https://matematykaszkolna.pl/strona/1543.html tg(α+β), tylko w naszym przypadku tg(α+α)

o rany julek: Kochany Broniaczku!

	a√2−2b
tg∡KDN=
	a√2+2b

I musisz już tylko popracować nad eleganckim przedstawieniem całego rozwiązania!