kombinatoryka
Blue: Odcinek PS jest średnicą okręgu. Na jednym półokręgu zaznaczamy punkty C
1 i C
2, a na
drugim półokręgu punkty C
3, C
4, C
5 i C
6 różne od punktów P i S. Rzucamy dwukrotnie
sześcienną symetryczną kostką. Jeśli wypadnie para różnych liczb oczek (m,n), gdzie
m∊{1,2,3,4,5,6}, to tworzymy kąt wpisany o ramionach C
mP i C
mC
n, a jeśli wypadnie
para (m,m), to tworzymy kąt wpisany o ramionach C
mP i C
mS. Oblicz prawdopodobieństwo
utworzenia w ten sposób kąta rozwartego, pod warunkiem, że co najmniej jedna z liczb
wyrzuconej pary oczek jest parzysta.
| | 2 | |
|
| , natomiast mi się wydaje, że |
| | 9 | |
15 kwi 13:58
Blue: 
15 kwi 16:58
Mila:
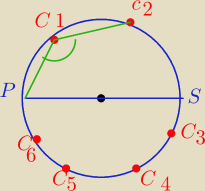
Wypisz kąty rozwarte:
PC
1C
2
...
15 kwi 17:05
Blue: Mila, mi chodzi o to, czy te kąty liczyć podwójnie, bo oni tak nie liczyli :
(1,2), (6,5), (5,4), (3,4), (3,6), (3,5), (4,6)
i (3,5) musimy tutaj odrzucić... i pytanie czy |AnB| = 12 czy 6
15 kwi 20:25
YushokU: nie mam kartki pod ręką, ale mi wychodzi że jest ich 6. Bo rozumiem Blue, że ty chcesz liczyć
(1,2) i (2,1) jako dwa osobne, prawda? Ale spójrz, że (1,2) spełnia warunki, a (2,1) nie.
| | 6 | | 2 | |
Więc jest ich 6, a wszystkich jest 27, więc P= |
| = |
| |
| | 27 | | 9 | |
15 kwi 21:20
Blue: Ej, rzeczywiście o.O Nie zwróciłam na to uwagi
Dziękuję
15 kwi 21:57
Mila:
Właśnie o to mi chodzi.
Kąt PC2C1 jest ostry, chciałam, abyś to zauważyła.
15 kwi 22:32
Mila:
Michał i Blue, przeliczcie to:
Dla jakich wartości parametru m równanie x2+(m+4)x+6m =0 ma dwa różne pierwiastki
rzeczywiste, których suma jest mniejsza od 15m−32?
15 kwi 22:38
YushokU: Założenia:
Δ>0
x
1+x
2<15m−32
Δ=m
2+8m+16−24m=m
2−16m+16
m
2−16m+16>0
Δ
m=192
√Δm=8
√3
m
1=8+4
√3
m
2=8−4
√3
m∊(8−4
√3;8+4
√3)
x
1+x
2=−(m+4)
−m−4<15m−32
16m>28
15 kwi 22:46
Benny: Mi wyszło, że m∊(8+4
√3;+
∞)
15 kwi 22:47
Mila:
Dziękuję kochani. Michał popraw odp.
Odpowiedź Bennego dobra.
Oj, przepraszam, ma być taka treść:
Dla jakich wartości parametru m równanie x2+(m+4)x+6m =0 ma dwa różne pierwiastki
rzeczywiste, których suma kwadratów jest mniejsza od 15m−32?
Mam wynik: (8+4√3,16)
Nie piszcie rozwiązania, tylko potwierdzenie lub podanie swojego wyniku.
15 kwi 22:56
YushokU: I masz rację
, bo ja robiłem to tutaj i schrzaniłem w myślach znak nierówność z deltą
15 kwi 22:56
Mila:
Benny, mam sporo nowych zadań dla poziomu R, ( nie wiem z jakiego zbioru).
Czy chcesz powalczyć?
Sporo rozwiązałam i jestem trochę oklapnięta.
15 kwi 22:58
YushokU: no to.
x12+x22=(x1+x2)2−2x1x2=m2+8m+16−12m=m2−4m+16
m2−4m+16<15m−32
m2−19m+48<0
Δm=169 √Δm=13
m1=16
m2=3
m∊(3;16)
m∊(8+4√3;16)
15 kwi 23:01
Benny: Wynik dobry
15 kwi 23:01
Benny: Jasne
15 kwi 23:02
Mila:
Dziękuję.
15 kwi 23:03
Mila:
Dla
Bennego i Michała
1) Wykaż, że równanie :
| x | |
| −sinx=0 ma co najmniej 3 pierwiastki w przedziale <−π,π> |
| 2 | |
Załóż nowy wątek;
15 kwi 23:11
YushokU:
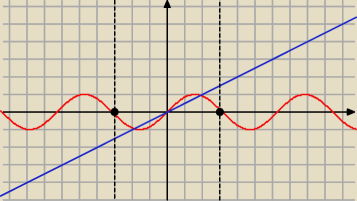
Chyba tylko można polegać na wykresie.
15 kwi 23:19
15 kwi 23:23
Mila:
Możesz wykorzystać metodę graficzną, ale trzeba skomentować.
1) x=0 jest rozwiązaniem
...
...
15 kwi 23:34
