Funkcja pochodna i parametr m Piotr: Wyznacz liczbę pierwiastków równania w zależności od parametru m, x⁴−2x²+1=m Nie mam pojęcia jak to zacząć, z góry dzięki!

J: podstaw: t = x² .... teraz: t² − 2t + 1 = m ⇔ (t −1)² = m ... i analizuj naszkicuj wykres (t − 1)² i popatrz w ilu punktach prosta: y = m przecina wykres

Piotr: z wykresu wynika że dla m(−∞,0) 0 rozw, dla m=0→1rozw a dla m (0,∞)→ 2 rozw, co się nie zgadzą sie z odpowiedzią...

J: bo teraz wracasz do równania wyjściowego twoje t = x² ...teraz pomyśl

silly goose: Czy ktoś mógłby to dokończyć? bo naprawdę nie potrafię tego zrobić

Filip: x⁴−2x²+1=m, m,x∊R (x²−1)²=m i dalej latwo wyznaczyc

silly goose: :')

silly goose: nie wiem skąd mają wyjść 4 rozwiązania...

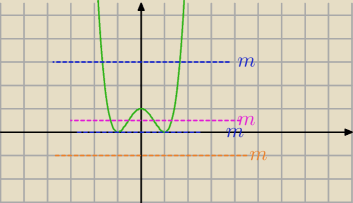
Qulka: rysujesz zielony wykres y= (x²−1)² a potem kolorowe y=m i jak widać dla m<0 pomarańczowe m się nie przetną z zieloną − nie ma rozwiązań dla m=0 i dla m>1 niebieskie m z zieloną spotykają się dwa razy − są dwa rozwiązania dla m=1 ....są 3 rozwiązania dla 0<m<1 fioletowe m przecina cztery razy zieloną

silly goose: Jak narysować samemu zielony wykres? czy mógłby ktoś napisać krok po kroku?

Filip: a po co? (x²−1)²=m m < 0 − brak rozwiazan (x²−1−√m)(x²−1+√m)=0 1) x²−1−√m 2) x²−1+√m Δ₁>0 i Δ₂>0 i m>0 4+4√m>0 i 4−4√m>0 i m>0 √m<1 i √m>0 m∊(0,1) − 4 rozwiazania −−− z tego wynika juz, ze m>1 −− dwa rozwiazania pozostalo sprawdzic dla m=0 i m=1 1) m=0 (x²−1)²=0 x=1 v x=−1 dwa rozwiazania 2) m=1 (x²−1)²=1 (x²−2)(x²)=0 x=0 v x=±√2 3 rozwiazania Podsumowujac: m<0 − brak rozwiazan m=0 i m>1 − dwa rozwiazania dla m=1 − trzy rozwiazania dla m∊(0, 1) − 4 rozwiazania

Qulka: I SPOSÓB skoro w tytule jest pochodna to liczysz pochodną z x⁴−2x²+1 4x³−4x i widzisz że na 3 miejsca zerowe x=−1, x=0 , x=1 sprawdzasz jak się zmieniają znaki i wiesz że masz min, max i min podstawiasz te x do wyjściowej funkcji żeby mieć jak wysoko sięgają i jak masz te 3 kropki i wiesz kiedy w górę a kiedy w dół to łączysz je mniej więcej i masz jak przebiega zielona bo potrzebujesz tylko ilość rozwiązań

Filip: tak teraz zauwazylem, ze skoro (x²−1−√m)(x²−1+√m)=0 i delta z pierwszego nawiasu wynosi 4+4√m co jest zawsze > 0 dla m>=0, to mozna rozpatrywac tylko drugi n awias i tam delte

Qulka: właśnie chciałam pisać II sposób z tym (t−1)² gdy t=x² ale masz wyżej

Filip: wiesz co... ja dopiero teraz zauwazylem to, jednak nie mam mozliwosci edycji mojej zamieszczonej odpowiedzi − tak to bym pewnie zmodyfikowal moje wywody na mniej chaotyczne

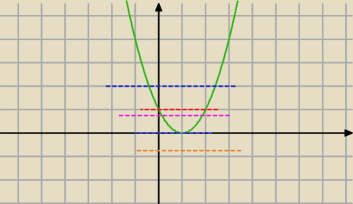
Qulka: albo narysuję II SPOSÓB jak masz zielone (t−1)² to widać że dla pomarańczowych m nie ma rozwiązań dla m=0 jedno t dodatnie więc potem dwa x bo t=1 czyli x²=1 czyli x=−1 lub 1 dla 0<m<1 dwa t dodatnie wic potem cztery x dla m=1 t=0 i t>0 więc trzy x dla m>1 jedno t dodatnie czyli dwa x i t ujemne czyli nie ma x bo x²<0 to sprzeczność

Qulka: też zapomniałam podpisać ze to oś t i dopisać kolorków przy m.. ale chyba widać o co biega

silly goose: mam straszny problem ze zrozumieniem tych zadań Robię teraz takie: Wyznacz dziedzinę i ekstrema funkcji. Naszkicuj wykres funkcji i odczytaj z niego zbiór rozwiązań nierówności f(x).>1.

	4x−8		16x−32
f(x)=x−2 −		−
	x−5		(x−5)2

Mam już prawie wszystko policzone: zał. x≠5i |q|<1 D: x∊(−niesk; 1)∪(9;+niesk)

	x2−7x+10
f(x)=
	(x−1)

	x2−2x−3
f'(x)=
	(x−1)2

maksimum w punkcie x=−1, f(−1)=−9 minimum w x=3 granica pionowa dla x=1 I pytanie jak policzyć/narysować tę funkcje, żeby mieć f(x)>1, które w odp jest dla x∊(9; niesk) nic mi nie wychodzi

Qulka: https://matematykaszkolna.pl/forum/408792.html

Qulka: tam masz obrazek (chociaż zapomniałam wyszarzyć te co nie łapią się na dziedziną a y=1 to tak jak te m w poprzednim zadaniu ... pozioma kreska.. i ze względu na dziedzinę ta zielona się zaczyna dużo wyżej i dlatego dopiero od x>9

Qulka: do sprawdzania obliczeń (i rysunków) https://www.wolframalpha.com/input/?i=%28x-2%29%2F%281%2B%284%2F%28x-5%29%29%29

Jerzy: @ mądra kaczko , poczytaj n/t badania funkcji. Ta procedura umożliwia naszkicowanie przybliżonego wykresu funkcji,który nie jest oczywisty.

silly goose: Dziękuje za pomoc

Filip: czy taka mondra bym polemizowal, natomiast silly goose z angielskiego na nasze to tak zwany "glupek" czy cos pokroju tego

silly goose: dzięks

Jerzy: 13:33 , "głupia gęś"