pomoc!! pawel93: Witam mam kilka zadan do zrobienia pomógł by ktoś ?

J: wrzucaj

pawel93: Środek okręgu o równaniu x² + y² − 10x + 8y − 80 = 0 ma współrzędne?

pawel93: Pole trójkąta równobocznego ma wierzchołek A= (−4,4) i B= (5,8) wynosi ?

pawel93: Wskaż równanie okręgu o środku o współrzędnych (4, −8) i promieniu 7

pawel93: Współczynnik kierunkowy prostej prostopadłej do prostej o równaniu y=4x−2 jest równy?

J: 1) ⇔ (x − 5)² − 25 + (y + 4)² − 16 − 80 = 0 ⇔ (x−5)² + (y−4)² = 11² S(5,−4) i promień: r = 11

Janek191: z.1 ( x − 5)² − 25 + ( y + 4)² − 16 − 80 = 0 (x − 5)² = ( y + 4)² = 11² S = ( 5, − 4) =========

J:

	a2*√3
2) oblicz długość boku AB = a ... potem PΔ =
	4

Janek191: Miało być ( x − 5)² + ( y + 4)² = 11²

J: 3) (x −4)² + (y +8)² = 49

pawel93:

	12
Wyznacz wartość tangensa kąta ostrego α wiedząc że cosinus kąta α wynosi
	13

J:

	1
4) a = −
	4

J:

	sinα
5) oblicz sinα z jedynki trygonometrycznej ... potem: tgα =
	cosα

pawel93:

	sin α−cos α
Wskaż wartość wyrażenia		wiedzac ze tg α =3
	sin α + cos α

J: może na razie wystarczy ... dość gotowców ... pokaż jak robisz zad 2)

J:

	sinα
zad 6) wskazówka: tgα =
	cosα

pawel93: Dany jest trójkąt prostokątny o przeciwprostokątnej równej 9 i przyprostokątnej 6 Cotangens kąta leżacego miedzy tymi blokami wynosi

pawel93: chodzi o to ze zbyt nie mam jak tego zrobic bo nie rozumiem... a jutro musze oddac prace...

J: no to sobie wcześnie przpomniałeś ... to nie jest forum dla leni ..

pawel93: dzieki ....

kwaśny: zadanie 3 tgα=3 więc sinα/cosα=3. stąd wynika, że sinα=3cosα. podstaw do wyrażenia (sinα−cosα)/(sinα+cosα) i otrzymasz (3cosα−cosα)/(3cosα+sinα)= 2cosα/4cosαeniu daje 2/4 czyli 0.5

J: nieźle namotałeś kwaśny ... wystarczy licznik i mianownik podzielić przez cosα

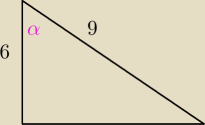
5-latek: nawet rysunku nie potrafisz zrobić TEraz co to jest cotangens ? czego to jest stosunek ?

pawel93:

6
	?
9

pawel93: a narysowany jest sin α ?

Kejt: zanim 5−latek zauważy... https://matematykaszkolna.pl/strona/397.html

5-latek: Narysowany jest cosα a nie sinus α napisz definicje cotangensa

5-latek: Czesc Kejt

Kejt: A niech to.. jednak zauważył Cześć (:

pawel93: Cotangensem kąta ostrego w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przyległej do kąta do długości drugiej przyprostokątnej

5-latek: To z twierdzenia pitagorasa oblicz dlugosc drugiej przyprostokątnej bo ona potrzebna jest do obliczenia cotangensa kata α

pawel93: 6² + b² = 9² ?

Kejt: teraz wylicz b

Braun: b∊R₊ b²=9²−6² b²=45 b=3√5 lub b=−3√5 odrzucam b=3√5 =====================

pawel93: 9² − 6² = b² 81−36= 45 ?

5-latek: CzescBraun Paweł jesteś w dobrych rekach korzystaj z tego

Braun: Witam.

Kejt: b = √45 teraz wyłącz liczbę przed pierwiastek.

pawel93: korzystam kiedys to umiałem ale kilka lat nie miałem matematyki i teraz w glowie nic nie mam ...

pawel93: no 3√5

5-latek: Dlaczego ? Rozpisz to zobaczymy czy to rozumiesz czy tylko przepisales

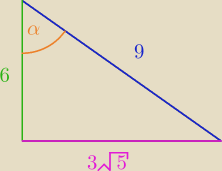
Kejt: ile wynosi cotangens?

pawel93:

	6
ctg
	3√5

Kejt: pudło...nie zgaduj tylko przemyśl.

Kejt: ok, mój błąd.

pawel93: no bo √45= √9*5 = 3√5

Kejt:

5-latek: No to teraz napisz ile wynosi tgα, cosα, i sinα

pawel93:

	3√5		6		3√5
tgα=		cosα=		sinα=
	6		9		9

Braun: Trochę kosmetyki.

	√5
tgα=
	2

	2
cosα=
	3

	√5
sinα=
	3

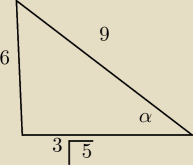
5-latek: Teraz zapisz sin α. cosα,tgα,ctgα

pawel93:

	6		3√5		3√5
sinα		? cosα		? ctgα		?
	9		9		6

5-latek: a tgα?

pawel93:

	6
tgα
	3√5

5-latek: No i gitara tylko staraj się gdzie to możliwe uproscic lub usuwac niewymiernosc z mianownika czy już trochę rozjaśnione ?

pawel93: tak juz lepiej Dziekuje

5-latek: Podziekuj jeszcze koleżance Kejt i koledze Braun za pomoc

pawel93: Dziekuje Wszystkim za pomoc! niestety pouczył bym sie dalej zadań lecz czas na mnie do pracy.. jutro oddanie zadan niestety za pozno sie obudzilem postaram sie wiecej razy odwiedzac tę strone bo mozna sie z niej duzo nauczyć dzieki takim osobom

Kejt: <kłania się>