matura 2015
Kacper:
Matura 2015
Podnosimy poziom.
Wyznacz te wartości parametru m, m∊R, dla których równanie
| | 1 | |
3x+1+3x+3x−1+...= |
| (4*32x+m) |
| | 8 | |
ma dokładnie jedno rozwiązanie.
6 kwi 20:57
Kacper:
Bardzo proszę o rozwiązania tylko maturzystów
(Dla innych to nic trudnego)
6 kwi 20:58
Blue: m=21
6 kwi 21:19
5-latek: Wolfram
6 kwi 21:22
Blue: To jaka jest odpowiedź?
6 kwi 21:24
Ajtek:
A co to za koszmarek?
6 kwi 21:30
Benny: Doszedłem do równania:
dla jednego rozwiązania pasują mi tylko dwa przypadki, ponieważ a>0
1)
Δ>0
t
1*t
2<0
2)
Δ=0
t
0>0
z 1) m<0
z 2) m=81
6 kwi 21:35
Blue: kurcze mam błąd rachunkowy xd zaraz jeszcze raz obliczę
6 kwi 21:40
Blue: tak, z warunku z deltą =0 wyjdzie 81
6 kwi 21:42
Marek: co zrobić z tym ... ?
6 kwi 22:32
daras: Kacper nie załamuj maturzystów
niech się skupia na tym co już pojęli dobrze
6 kwi 22:34
daras: moich zadań nikt wszystkich nie rozwiązał a były łatwiejsze
6 kwi 22:45
Benny: Moje rozwiązanie jest złe?
6 kwi 22:51
daras: @Benny fizykę tez zdajesz?
6 kwi 22:58
Benny: tak
6 kwi 23:05
6 kwi 23:10
Saizou : jak dobrze że ja już nie muszę fizyki się uczyć
6 kwi 23:11
Benny: No umiem trochę tych wzorków, ale na wiki coś nie tak podpatrzyłem teraz
6 kwi 23:12
Martiminiano: | | 1 | |
Mnie wyszło m=20 |
| . Jaka jest odpowiedź? |
| | 4 | |
7 kwi 00:23
Martiminiano: Błąd rachunkowy... m=81.
7 kwi 01:02
Kacper:
Odpowiedź to: m∊(−∞,0>∪{81}.
7 kwi 07:17
Benny: Czyli moja odpowiedź była prawidłowa?
7 kwi 10:24
Martiminiano: A czy mógłby ktoś zamieścić jak powinno wyglądać prawidłowe rozwiązanie?
7 kwi 10:48
Benny: Całe od początku? Czy od równania chcesz?
7 kwi 10:50
Martiminiano: Musiałem wtedy już iść, a później rozwiązywałem próbne matury i dopiero teraz jestem.
W sumie to nie wiem dlaczego jest ten warunek z Δ>0, byłbym wdzięczny gdybyś mi to wyjaśnił
8 kwi 01:02
Benny:
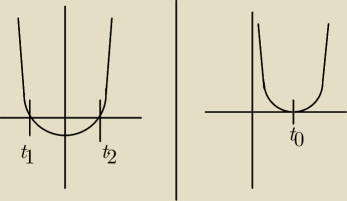
Traktujesz to jako równanie kwadratowe i podstawiasz za 3
x=t
t>0
jeśli ma być jedno rozwiązanie to masz dwa przypadki
w pierwszym przypadku Δ>0, t
1 jest ujemne, co jest sprzeczne z założeniem, więc mamy tylko
jedno rozwiązanie t
2
w drugim przypadku mamy tylko jedno rozwiązanie dla t
0>0 i Δ=0
no i sprawdzamy dla m=0 czy równanie ma rozwiązania i dostajemy
m∊(−
∞;0> ∪{81}
8 kwi 16:27
Martiminiano: Pięknie, dziękuję bardzo
8 kwi 20:36