zadanie optymalizacyjne Archy: Opakowania na frytki w kształcie rożka wykonuje się z wycinka koła o promieniu r. Opakowanie ma takie wymiary, że jego pojemność jest możliwie największa. Oblicz wysokość i promień podstawy stożka będącego wzorcem opakowania.

Archy:

daras: czy to jest torus, banan czy dętka ? nie jadam frytek więc nie wiem

Archy: To jest zwykly stozek...

daras: to w czym problem https://matematykaszkolna.pl/strona/1003.html

Archy: problem w tym że nie mogę sobie poradzić z funkcją którą ułożyłem.

	1		α		α
wyszło mi v=		*π*(R(1−		))2*R−R(1−		) gdzie R to promień tego okręgu
	3		360		360

wyjściowego

daras: nie jest to wycinek koło tylko kuli i dalej idź tym tropem

daras: + r² = h² + R²

daras: a funkcja do pobadania wygląda tak:

	1
V =		πR2√r2 − R2
	3

otwórz sobie albo poszukaj na chomiku Krysickiego, Włodarskiego w t.1 jest bodajze takie samo zadanie, kiedyś to dawali na maturze

Archy: dlaczego kuli jak w trści zadania pisze że z wycinka koła?

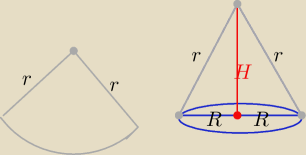
Eta: r=l −− dł. tworzącej stożka H=√r²−R² , R<r i H<r

	1
V(R)=		πR2*√r2−R2
	3

V^'(R)=0 ⇒ ............. dokończ.........

Archy:

	2		1
v"(R)=		πR*		(r2−R2)*2r*2R
	3		2

Archy:

	1
pomyłka.		(r2−R2)u−{1}{2}
	2

Archy: czyli do 0 trzeba przyrównać 2πR*2*(2r−2R)

Archy: nie wiem jak to skończyć. Z tej pochodnej nie wyjdą mi miejsca zerowe

Eta:

	1		2R
V'(R)=		π[2R*√r2−R2−R2*		] =0 /*3π
	3		2√r2−R2

	R3		√r2−R2
2R*√r2−R2−		=0 /*
	√r2−R2		R

2(r²−R²)−R²=0 ⇒ 3R²=2r² ⇒ R=.................. i H=.............

daras: a co ja napisałem o 14:14 jak to nie wyjdą ci miejsca zerowe powtórz sobie wszystko najpierw a potem pytaj, bo jak nic nie umiesz, to trudno coś wytłumaczyc

Eta: