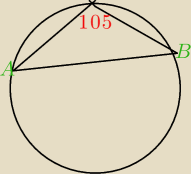
f msp: Promień okręgu jest równy 4√2 oblicz długość cięciwy AB. myślałem nad użyciem twierdzenia o kątach w okręgu ale nie wiem jak go tu użyć

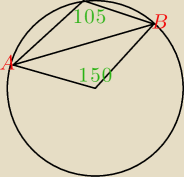
msp: skąd wiadomo, że kąt między promieniami poprowadzonymi od środka do punktów A i B ma 150 stopni?

Saizou :

1
	α=105
2

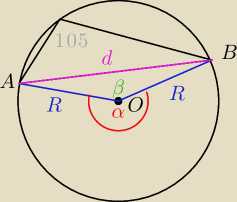
α=210⇒β=360−210=150 i z tw. Carnota

	√3
d2=R2+R2−2R2cos150 cos150=cos(90+60)=−sin60=−
	2

	√3
d2=32+32−2*32*(−		)
	2

d²=64+32√2 d=√64+32√2

Saizou : a to wiadomo stąd https://matematykaszkolna.pl/strona/465.html

msp: dziekuje bardzo

Benny:

x
	=sin75o
R

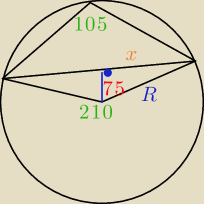
x=cos15^o*R

	√6+√2
x=		*4√2
	4

x=2(√3+1) |AB|=4(√3+1)

Benny: kurde a myślałem, że dobrze mam

Benny: Nie no dobrze mam u Ciebie jest mały błąd pod pierwiastkiem powinien być chyba √3 a nie √2

Benny: Ktoś sprawdzi?

Saizou : tak, masz rację, powinno być d=√64+32√3=√(4√3+4)²=4√3+4