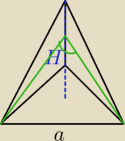
 Dany jest ostrosłup prawidłowy trójkątny. Stosunek długości wysokości ostrosłupa do długości
krawędzi jego podstawy jest równy √66 . Wykaż, że kąt między sąsiednimi ścianami
bocznymi tego ostrosłupa jest prosty.
Prosiłbym o pomoc w rysunku i pomoc jak na to mogę spojrzeć i jak obliczyć.
Rysunek nie jestem pewny, ale chyba źle wykonałem.
Dany jest ostrosłup prawidłowy trójkątny. Stosunek długości wysokości ostrosłupa do długości
krawędzi jego podstawy jest równy √66 . Wykaż, że kąt między sąsiednimi ścianami
bocznymi tego ostrosłupa jest prosty.
Prosiłbym o pomoc w rysunku i pomoc jak na to mogę spojrzeć i jak obliczyć.
Rysunek nie jestem pewny, ale chyba źle wykonałem.
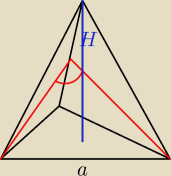 Wykonałem rysunek. Nie jestem dalej pewny czy dobrze zaznaczyłem kąt.
Krawędź podstawy jest a.
Wtedy wysokość jest równa H = a√6 przez 6
Co teraz powinienem policzyć?
Wykonałem rysunek. Nie jestem dalej pewny czy dobrze zaznaczyłem kąt.
Krawędź podstawy jest a.
Wtedy wysokość jest równa H = a√6 przez 6
Co teraz powinienem policzyć?
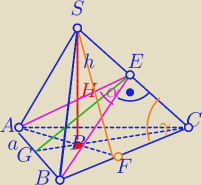
| H | √6 | ||
= | |||
| a | 6 |
| a√6 | ||
H= | ||
| 6 |
| 1 | a√3 | a√3 | ||||
|PF|= | * | = | ||||
| 3 | 2 | 6 |
| a√3 | a√6 | |||
h2=( | )2+( | )2 | ||
| 6 | 6 |
| a2*3 | a2*6 | a2 | ||||
h2= | + | = | ||||
| 36 | 36 | 4 |
| a | ||
h= | ⇔ΔSFC− Δprostokątny równoramienny⇔γ=45o | |
| 2 |
| a | ||
|BF|= | ||
| √2 |
| α | 12a | |||||||||
sin | = | ⇔ | ||||||||
| 2 |
|
| α | √2 | α | ||||
sin | = | ⇔ | =45o | |||
| 2 | 2 | 2 |