zadanka Blue: zad.1 Udowodnij, że jeżeli punkt D jest środkiem ciężkości trójkąta, to −> −> −> −> DA + DB + DC = 0. zad.2 Mógłby mi ktoś powiedzieć, czy to jest dobrze rozwiązane? http://i61.tinypic.com/29y143q.jpg

Blue:

Saizou : a co wiesz o środku ciężkości ?

Blue: Wiem, co to jest środek ciężkości, jest to przecięcie środkowych i ten środek ciężkości dzieli każdą z nich w stosunku 2:1, ale jak to rozwiązać?

Eta: https://matematykaszkolna.pl/forum/172822.html

YushokU: A jakby tak wpisać to w układ współrzędnych i skorzystać z wzoru na środek ciężkości? Wyobrażając sobie to wychodzi mi całkiem ładne i proste rozwiązanie

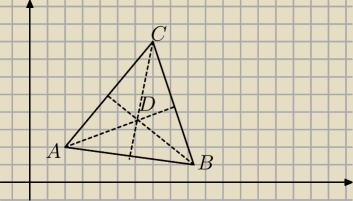
YushokU: A(x_a,y_a) B(x_b,y_b) C(x_c,y_c)

	xa+xb+xc		ya+yb+yc
D(		,		)
	3		3

	xa+xb+xc		ya+yb+yc
DA→=[xa−		;ya−		]
	3		3

	xa+xb+xc		ya+yb+yc
DB→=[xb−		;yb−		]
	3		3

	xa+xb+xc		ya+yb+yc
DC→=[xc−		;yc−		]
	3		3

	xa+xb+xc		ya+yb+yc
DA→+DB→+DC→[(xa+xb+xc−3		;ya+yb+yc−3		]=0→
	3		3

Blue: Dziękuję Wam

Blue: A mógłby jeszcze ktoś powiedzieć mi czy to zadanie 2 jest ok?

YushokU: Hmmm.. zaraz sprawdzę i przy okazji pokażę dobry sposób na zadanka tego typu

YushokU:

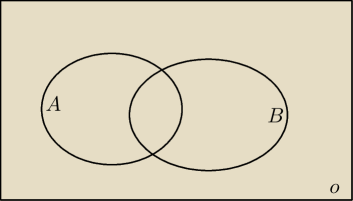
	4		3		1
Wykaż, że jeżeli A,B są podzbiorami Ω oraz P(A)<		, P(A∪B)>		, to P(A∩B')<		.
	7		8		5

Z schematu widzimy, że: P(A∩B')=P(A\B) P(A\B)=P(A)−P(A∪B) Znak daję na logikę

	4		3
P(A\B)<		−
	7		8

	11		1
P(A\B)<		<
	56		5

Ja bym tak to zrobił. W twoim rozwiązaniu ja nie do końca widzę, co się tam dzieje i skąd to się bierze, ale tak to już czasem z kombinatoryką i prawdopodobieństwem jest No i masz literówkę w zapisie.

Mila: Nie chce mi się otworzyć stronka z zadaniem, ale , czy dobrze treść przepisałeś? Wydaje mi się, że o to chodzi: http://www.zadania.info/d487/9095970

Blue: A no tak , mam literówkę rzeczywiście, ale to niechcący Ale ogólnie to dobrze myślałam

YushokU: Jasne, że źle Potem już sobie tylko to kopiowałem i mi się powieliła

YushokU: Swoją drogą, to mam identyczne rozwiązania jak na zadania.info, niemalże co do słowa Obydwa