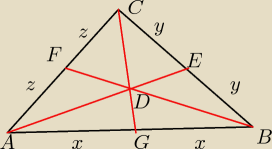
matura PuRXUTM: Udowodnij że jeżeli punkt D jest środkiem ciężkości trójkąta ABC, to DA→ + DB→+DC→=0→ coś próbowałem kombinować ale nic nie wyszło...

Andrzej: Środek ciężkości dzieli każdą środkową w stosunku 2 : 1 licząc od wierzchołka, czyli |CD| = 2|DG|, a pisząc wektorami CD→ = 2DG→, ale CD→ = −DC→ czyli DC→ + 2DG→ = 0→ G to środek boku AB, czyli GA→ + GB→ = 0→ DA→ = DG→ + GA→ DB→ = DG→ + GB → więc Twoja suma to: (DG→ + GA→) + (DG→ + GB→) + DC→ = = 2DG→ + DC→ = 0→

PuRXUTM: dzięki wielkie