zadanka
Benny: Coś nie za bardzo lubię te dowody geometryczne. Jutro jakąś próbną rozszerzoną piszemy,
zobaczymy co tam będzie

25 mar 21:31
25 mar 21:35
Benny: Musze porobić trochę tych dowodów geometrycznych, bo dziś znowu był dowód z dwusieczną w
trójkącie prostokątnym, środkową i wysokością. Myślałem coś o okręgu opisanym, ale nie
napisałem nic, ale pomysł był dobry. No i przypomniało mi się że nie napisałem znowu
odpowiedzi do zadania

26 mar 17:10
prosta:
jakąś próbną ogólnoszkolną ? czy jakąś okręgową?
26 mar 17:56
prosta:
zadanie 7....bajka

26 mar 17:57
Benny: Lubelska rozszerzona, taaa zadanie 7 bajka, ale nie wiem czy to przez stres czy przez co
zawiesiłem się przy układzie równań

26 mar 18:07
Benny: A co myślisz o tym zadaniu z prawdopodobieństwa?
26 mar 18:10
prosta:
prawdopodobieństwo to już niezłe wyzwanie....nie podejmę się rozwiązania

26 mar 18:29
Benny: czego tego zadanka tak nikt nie lubi

26 mar 18:29
26 mar 18:32
Benny: Też mi się tak wydaję, tylko to udało mi się wymyślić
26 mar 18:34
Benny: Tak sobie myślę, że mało czasu zostało, więc jak zdam maturę to trzeba będzie jakieś studia
wybrać, ale nie mam żadnego pomysłu

Wychowawczyni(od matmy) mówiła, żebym kombinował coś z
matmą stosowaną, myślałem o tym, ale co można po tym robić? Co tu robić?

28 mar 08:14
Qulka: tak jak po każdych innych studiach

wszystko

studia są po to by udowodnić pracodawcom, że
umiesz się SAM zorganizować , nauczyć i dobrze wykonać zadania

28 mar 08:21
Benny: "Sam" zorganizować, ale gdzie? w czym?

28 mar 08:29
Qulka: najlepiej wybierać to co lubisz

będzie dużo łatwiej

w obecnej erze informatycznej i tak pracę zmienisz kilkanaście razy z kierunek działań pewnie
ze 3 więc najważniejsza jest elastyczność i umiejętność dostosowania do zmian i szybkiej
organizacji się w nowym miejscu (czyli to co masz na każdych studiach )
28 mar 11:16
Benny: Pani
Mila może jest? Może jakieś zadanko do zrobienia jest?

29 mar 20:36
Mila:
1) Rozwiąż nierówność:
|2x−5|−|x+5|≤2−2x
2) Rzucamy 4 razy kostka sześcienną do gry.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb oczek otrzymanych we
wszystkich 4 rzutach jest równy 60.
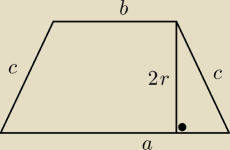
3) Trapez równoramienny ABCD o podstawach AB i CD jest opisany na okręgu o promieniu r.
wykaż, że 4r2=|AB|*|CD|
29 mar 20:49
Benny:
1) x∊(−
∞;−8>∪<−5;4>
2)
|Ω|=6
4
tutaj będą takie możliwości:
(1,2,5,6)−>4!
(1,3,4,5)−>4!
|A|=60
3)
| | a−b | |
w tym trójkącie prostokątnym mamy przyprostokątne o długości 2r i |
| |
| | 2 | |
okrąg wpisany w trapez, więc a+b=2c
16r
2=a
2+b
2+2ab−a
2−b
2+2ab
16r
2=4ab
4r
2=ab
29 mar 21:17
Mila:
2 i 3) dobrze.
Sprawdzam (1)
29 mar 22:13
Mila:
1) x∊(−∞;−8>∪<−2;4>
29 mar 22:19
Benny: źle przepisałem, oczywiście powinno być −2

29 mar 22:23
Mila:
4). W graniastosłupie prawidłowym sześciokątnym najdłuższa przekątna podstawy ma długość d
i tworzy z przekątną ściany bocznej wychodzącą z tego samego wierzchołka kąt o mierze a.
Wyznacz objętość graniastosłupa.
29 mar 22:33
Mila:
5) Wykaż,że jeżeli jeden z kątów trójkąta ma miarę 30o, to długość boku przeciwległego temu
kątowi jest równa promieniowi okręgu opisanego na tym trójkącie.
30 mar 15:04
Benny:
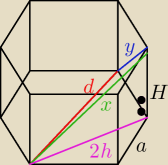
między czerwoną a niebieską linią jest kąt α
x
2=H
2+(2h)
2
a
2+H
2=y
2
x
2=y
2+d
2−2dycosα
2h=a
√3
| | d√1−4cos2α | |
po rozwiązaniu tego układu wyszło mi H= |
| |
| | 4cosα | |
Dziwny wynik

30 mar 15:22
Benny: W tym 5 to tw.sinusów i tyle?
30 mar 15:25
Mila:
Bardzo dobrze.
30 mar 15:31
Mila:
Zastanawiam się nad rysunkiem. Odezwę się w tej sprawie.
30 mar 15:34
Mila:
+
30 mar 16:52
Benny: 
30 mar 17:02
Mila:
6)
Wyznacz i zapisz dziedzinę funkcji jako sumę przedziałów.
f(x)=log(2cosx)(9−x2)
7) Wyznacz wszystkie rozwiązania równania:
2cos2x=cosx dla x∊<0,2π>
30 mar 21:17
Benny: zad. 6
| | π | | π | | π | | π | | π | | π | |
x∊(− |
| ;− |
| )∪(− |
| ; |
| )∪( |
| ; |
| ) |
| | 2 | | 3 | | 3 | | 3 | | 3 | | 2 | |
zad. 7
| | π | | π | | 3π | | 5π | |
x= |
| ∨ x= |
| ∨ x= |
| ∨ x= |
| |
| | 3 | | 2 | | 2 | | 3 | |
30 mar 21:42
Mila:
Dobrze.

30 mar 22:02
Benny: Cieszę się

30 mar 22:07
Mila:
8)
Jeżeli od 4 wyrazów ciagu geometrycznego odejmiemy odpowiednio kolejne wyrazu ciągu
arytmetycznego, to otrzymamy liczby:1,4,17,50.
Wyznacz ten ciąg geometryczny.
30 mar 22:37
Benny: pierwszy wyraz ciągu geo. − a
1
pierwszy wyraz ciągu ar. − a
1'
a
1−a
1'=1
a
1−1=a
1'
więc a
2'=a
1−1+r itd.
a
1*q−a
1+1−r=4
a
1(q−1)=r+3
a
1*q
2−a
1+1−2r=17
a
1(q
2−1)=16+2r
a
1(q
3−1)=49+3r
a
1=10
q=2
Dwa razy rozwiązywałem ten układ, bo za pierwszym jakoś dziwnie podstawiałem

30 mar 23:16
Benny: Tym zadankiem kończę dzisiejszy dzień. Dobranoc

30 mar 23:21
Mila:
Szybko rozwiązałeś.
Dobranoc

30 mar 23:38
Benny: Może dlatego, że mój mózg pragnął odpoczynku?

31 mar 17:56
Mila:
Jest indeks?
31 mar 18:07
Benny: Nima i nie będzie. Wyniki chyba dopiero 20 kwietnia. Coś fajnego jest dziś do zrobienia?
31 mar 18:42
Mila:
Myślę,że będzie. Zadania znajdę. Za chwilę.
31 mar 20:31
Mila:
1) Podaj liczbę rozwiązań równania w zależności od parametru m
|x2−6x+8|+|x2−6x+5|=m
31 mar 20:51
Benny: Rozpisywanie tego na przedziały raczej nie będzie dobrym pomysłem. Oczywiście m na pewno nie
jest mniejsze od 0

31 mar 22:06
Mila:
Rysowanie f(x) w przedziałach, bardzo ładnie to wychodzi, trzeba troche cierpliwości.
31 mar 22:19
Benny: Tylko trochę długo. Inne sposoby są? Bo nie wiem czy coś innego próbować.
31 mar 22:31
Mila:
Ja rozwiązałam rozpisując wzór funkcji na przedziały. Narysowałam wykresy.
Szukaj innych sposobów.
31 mar 22:38
Benny: hmm to z tych przedziałów wychodzi tak:
m∊(5;+
∞), dwa rozwiązania
m=5, trzy rozwiązania
m∊(3;5), cztery rozwiązania
i tutaj dla m=3 nie mam pomysłu jak to zapisać, bo mam 2 odcinki funkcji stałej

31 mar 23:05
Mila:
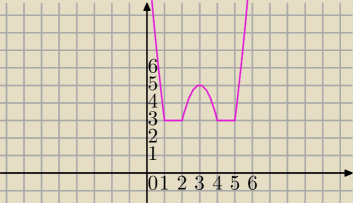
f(x)=3 dla x∊<1,2> lub x∊<4,5>
Dla m=3 istnieje nieskończenie wiele rozwiązań.
31 mar 23:24
Benny: No właśnie tak myślałem, ale wolałem się upewnić

31 mar 23:25
Benny: Jak będziesz miała jeszcze czas to poprosiłbym o jakieś zadanko. Mykam spać.
Dobranoc

31 mar 23:48
Mila:
2) W(x) =x
3+bx
2+cx+d ma 3 pierwiastki tworzące ciąg geometrycny o pierwszym wyrazie równym 2.
wiadomo, że W(3)=5
Znajdź te pierwiastki.
Dobranoc

1 kwi 00:01
Benny: Tak jak myślałem

maturka, zadanie z optymalizacji −1 pkt za brak oznaczeń, prawdopodobieństwo −2(całość)
pomyliłem kolory, −3 pkt dowód, który był prosty, ale nie wpadłem na pomysł i −1 pkt za
udowodnienie, że liczba jest podzielna przez 16.
Otrzymałem takie wyrażenie 8*(n+1)(n
2+2n+2) i napisałem, że dla n nieparzystych n+1 jest
podzielne przez 2, a dla n parzystych n
2+2n+2 jest podzielne przez 2 a powinienem napisać że
jeśli jest parzysta to n=2k a jak jest nieparzysta to n=2k+1. Czemu za mój sposób nie
otrzymałem pkt?
Co do Twojego zadanka to otrzymałem trzy ciągi:
x
1=2, x
2=−2, x
3=2
x
1=2, x
2=4, x
3=8
1 kwi 15:57
Mila:
1) Ciągi dobre.
2) Musisz zapytać sprawdzającego.
1 kwi 16:09
Benny: No pytałem i dowiedziałem się że tak to powinienem zapisać

1 kwi 16:10
Mila:
Znajdę zadania na podzielność;
Mam dwa w tej chwili.
Pisz całe rozwiązanie.
1) Wykaż, że liczba postaci:
(10n+2)2 jest podzielna przez 9 dla n∊N+
2) Wykaż, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.
1 kwi 16:25
Mila:
3)
Wykazać, że n5 – n, gdzie n jest liczb naturalną, jest podzielne przez 30.
4)
Wykazać, że n6 – 2n4+n2, gdzie n jest liczb naturalną, jest podzielne przez 36 dla n∊N.
5) Czy liczba
2*9100−999−998 jest podzielna przez 19?
Prosimy Etę o zadanka z podzielności.
==============================
1 kwi 16:33
Benny: liczba 10n+2 jest podzielna przez 3 ponieważ jest postaci 1000....2, więc jej kwadrat jest
podzielny przez 9
1 kwi 16:38
Benny: 4)n6−2n4+n2=n2(n4−2n2+1)=n2(n2−1)2=(n(n−1)(n+1))2
iloczyn trzech liczb naturalnych jest podzielny przez 6 więc ich kwadrat dzieli się przez 36
5)2*9100−999−998=998*(162−9−1)=152*998=8*19*998
1 kwi 16:52
Mila:
1) Suma cyfr liczby : 10n+2 jest równa 3, zatem liczba ta dzieli sie przez 3, więc jej kwadrat
dzieli się przez 9.
1 kwi 16:56
Benny: to 2 i 3 łeee
robię, robię i coś mi nie wychodzi, dostaje równanie 3n(n2+2) i tak jak wcześniej myślę sobie
o parzystej i nieparzystej, liczę, liczę i coś jest nie tak, liczba ma się dzielić przez 3,
więc robimy n=3k lub 3k+1 lub 3k+2
no i mamy:
2)
n=3k
9k(9k2+2)
n=3k+1
9(3k+1)(3k2+2k+1)
n=3k+2
9(3k+2)(3k2+4k+2)
3)
tutaj wychodzi mi n(n−1)(n+1)(n2+1) na razie mam, że dzieli się przez 6 coś z tym n2+1 trzeba
udowodnić, że dzieli się przez 5 czy jakoś inaczej?
1 kwi 19:06
ja: punkt A=(0,5) jest wierzchołkiem prostokąta ABCD. Osiami symetrii tego prostokąta są proste o
równnaniach y=1/2x+15/8 oraz y=−2x+15. Wyznacz równanie prostej zawierającej przekątną BD tego
prostokąta
Pomoże mi ktoś? proszę

1 kwi 19:11
Eta:
2/
podpowiedź

3n(n
2+2) = 3n[(n
2−1)+3] = .........
1 kwi 19:32
Benny: Widzę, że mój sposób jest dłuższy

więc mamy:
2)
3n[(n−1)(n+1)+3]=3n(n−1)(n+1)+9n
9n na pewno dzieli się przez 9, a 3n(n−1)(n+1) też dzieli się przez 9, ponieważ wśród 3
kolejnych liczb naturalnych jedna jest podzielna przez 3

Dzięki temu znalazłem analogie do 3

3)
n(n−1)(n+1)(n
2+1)=n(n−1)(n+1)[(n
2−4)+5]=n(n−1)(n+1)(n+2)(n−2)+5n(n−1)(n+1)
n(n−1)(n+1)(n+2)(n−2) to wyrażenie dzieli się przez 30, ponieważ jest to 5 kolejnych liczb
naturalnych, więc jedna na pewno dzieli się przez 2,3,5
5n(n−1)(n+1) to wyrażenie dzieli się przez 30, ponieważ są tu 3 kolejne liczby naturalne z
których jedna na pewno dzieli się przez 2 i przez 3
1 kwi 20:04
Eta:


1 kwi 20:07
Benny: Teraz na pewno będę takie rzeczy zauważał w tych dowodach

1 kwi 20:12
Eta:
To teraz zmierz się z takimi zadankami :
zad1/ Wykaż ,że dla każdego n∊N
| | 1 | |
liczba 4n+9n+3√ |
| *6n+1 jest kwadratem liczby całkowitej |
| | 27 | |
zad2/ Wykaż ,że liczba 7
2015−3
2016 jest podzielna przez
5
zad3/ Wykaż ,że liczba 7777
5+444
4−33
21 jest podzielna przez
10
zad4/ Wykaż ,że liczba 2
log35−5
log32 jest liczbą parzystą
zad5/Wykaż,że dla n∊N liczba (n−2)
4−n
4 jest podzielna przez
8
| | n4 | | n3 | | n2 | |
zad6/ Wykaż,że liczba |
| + |
| + |
| |
| | 4 | | 2 | | 4 | |
jest kwadratem liczby naturalnej
P.S. zadania
tylko dla
Benny !
Powodzenia

1 kwi 20:19
Eta:
Czekałam na .........magiczne słowo

znasz takie?
1 kwi 20:20
Benny: Dziękuję!

1 kwi 20:21
Eta:

1 kwi 20:24
Benny: Zad 1
| | 1 | |
4n+9n+ |
| *6n+1=22n+32n+2*6n=(2n+3n)2 |
| | 3 | |
Zad 2
Podobne zadanko było na AGH−u, więc zrobiłem analogicznie.
Co czwarta potęga cyfra jedności jest taka sama(dla każdej liczby?)
więc 7
2015 ma cyfrę jedności "3"
3
2016 ma również cyfrę jedności "3"
więc jak odejmiemy: 3−3 otrzymamy cyfrę jedności 0. Liczba, która kończy się cyfrą 0 dzieli się
przez 5. Takie wytłumaczenie wystarczy?
1 kwi 20:33
Eta: ok

1 kwi 20:43
Mila:
Powodzenia

Ładne zadanka
Eto.
1 kwi 20:47
Benny: Zad 5
(n−2)
4−n
4=((n−2)
2−n
2)((n−2)
2+n
2)=(n
2−4n+4−n
2)(n
2−4n+4+n
2)=8(1−n)(n
2−2n+2)
Zad 6
| n4+2n3+n2 | | n2(n2+2n+1) | | n2(n+1)2 | | n(n+1) | |
| = |
| = |
| =( |
| )2 |
| 4 | | 4 | | 4 | | 2 | |
Teraz muszę pomyśleć nad tym 3 i 4

1 kwi 20:54
Eta:
| | n(n+1) | |
Do zad. 5 .........jeszcze komentarz ,że |
| jest całkowita |
| | 2 | |
1 kwi 20:59
Mila:
w (6) przydałby się komentarz, masz tam ułamek w nawiasie.
1 kwi 21:01
Eta:
Oczywiście chodzi o zad 6 ( sorry)
1 kwi 21:02
Eta:
Mila .... zaraz znów Ci się ode mnie ...."oberwie"

1 kwi 21:04
Mila:
Eta jak ETA.
1 kwi 21:09
Eta:
ETA ! ... w Hiszpanii

1 kwi 21:13
5-latek: Witam Panie

Pozdrawiam


Poza tym obowiazuje ustawa o bezstresowym wychowaniu

1 kwi 21:13
Benny: Ok to będzie chyba tak, że iloczyn dwóch kolejnych liczb jest podzielny przez 2, więc
| | n(n+1) | |
|
| jest liczbą całkowitą |
| | 2 | |
1 kwi 21:20
Benny: Zad 4
Tutaj się tak męczyłem z początkiem, zapomniałem jak potęgi zamienić na logarytmy

2
log35−5
log32
2
log35=a
5
log32=b
log
32
log35=log
3a
log
35*log
32=log
3a
log
35
log32=log
3b
log
32*log
35=log
3b
log
3b=log
3a
a=b
a−b=a−a=0
Zadanko 3
nie mam już chyba pomysłów, wyłączanie, jakieś dziwne kombinowanie, skończyłem na
przedstawieniu tych liczb za pomocą sumy ciągu

2 kwi 11:03
Eta:
Witam

A jak rozwiązywałeś zad.2/ ?
to 3/ identycznie

2 kwi 11:17
Benny: No myślałem nad takim rozwiązaniem, ale bez kalkulatora ciężko określić cyfrę jedności 77775
lub 4444
2 kwi 11:21
Eta:
Liczba 7777 kończy się 7 to potęgi tej liczby kończą się:
77771= 7777
77772= .....9
itd
powtarzają się co 4 sekwencje
podobnie 4444 i 3321
...... dokończ
2 kwi 11:28
Benny: Wiem, że powtarzają się co 4, napisałem chyba wyżej. Jak patrzę na duża liczbę zawsze brać
tylko ostatnią cyfrę do potęgi aby sprawdzić jaką cyfrą się kończy, jeśli tak to będzie łatwo

Liczba 7777
5 kończy się 7, liczba 444
4 kończy się 6 a liczba 33
21 kończy się 3 więc 7+6−3=10
liczba 7777
5+444
4−33
21 kończy się cyfrą 0 więc dzieli się przez 10
2 kwi 11:55
Eta:
Dokładnie tak

2 kwi 12:49
Eta:
Masz ochotę na następną porcję zadań tego typu?
2 kwi 12:50
Benny: Coś możemy jeszcze spróbować
2 kwi 12:51
Eta:
zad1/ Wykaż ,że liczba 2015
2+2015
2*2016
2+2016
2
jest kwadratem liczby naturalnej
zad2/ Wykaż,że liczba 2
2012−16 jest podzielna przez 15
zad3/ Wykaż,żedla n∊N
liczba (n+1)(n+2)(n+3)(n+4)+1 jest kwadratem pewnej iczby naturalnej
zad4/ Wykaż ,że kwadrat każdej liczby naturalnej n
można przedstawić w postaci 3k lub 3k+1 , gdzie n,k∊N
zad5/ wykaż,że zachodzi równość 7
√log73=3
√log37
Powodzenia

2 kwi 13:03
Benny: Zad 1
tutaj zrobiłem tak 2015=x 2016=x+1
x2+x2(x+1)2+(x+1)2=x4+2x3+3x2+2x+1=x4+x3+x3+x2+x2+x2+x+x+1=
=x2(x2+x+1)+x(x2+x+1)+x2+x+1=(x2+x+1)(x2+x+1)=(x2+x+1)2
(20152+2016)2
Tak to może być? Czy jest inny sposób?
2 kwi 13:38
Benny: hmm co do zadania 2 nie jestem pewny
zad 2
22012−16=24(22008−1)
22008 −1 ma na końcu 5, więc dzieli się przez 5
Sprawdziłem sobie jak jest z podzielnością przez 3 i wyszło mi, że jak 2 podniesiemy do potęgi
parzystej i odejmiemy 1 to liczba będzie podzielna przez 3. 2008 jest parzyste, więc
22012−16 dzieli się przez 15
2 kwi 13:52
Benny: Zad 3
(n+1)(n+2)(n+3)(n+4)+1=n4+10n3+35n2+50n+25
analogicznie jak zad 1
n2(n2+5n+5)+5n(n2+5n+5)+5(n2+5n+5)=(n2+5n+5)2
2 kwi 13:59
Eta:
1/ ok (ale też można wykazać bez podstawienia)
2/ "sprawdziłem sobie" ................ Ty masz to uzasadnić( by sprawdzający dał Ci max
punktów
24(22008−1)= 24 (16502−1) = 16*(16−1)(16501+16500+.......+1)=16*15*k
2 kwi 14:00
Benny: Kurcze właśnie kombinowałem z tym wzorem, ale nie wpadłem, żeby 2 zamienić na 16

2 kwi 14:02
Eta:
3/ ok

można też tak :
(n+1)(n+4)(n+2)(n+3)+1= (n
2+5n+4)*[(n
2+5n+4)+2]+1= .........
2 kwi 14:02
Eta:
W iloczynie ma się pojawić czynnik
15
to myślisz w którym się pojawi? ... ano w (2
2008−1)
zatem (16−1) i .......... już wtedy wiesz jak jak działać

2 kwi 14:07
Benny: Też chce widzieć od razu te szybsze sposoby

2 kwi 14:09
Eta:
Z czasem nabierzesz wprawy ........ "trening czyni mistrza"

2 kwi 14:11
Eta:
do zad3/ uogólnienie:
iloczyn czterech kolejnych liczb naturalnych powiększony o 1
jest kwadratem liczby naturalnej
2 kwi 14:14
Eta:
100 moja

2 kwi 14:15
Qulka: Eta 

2 kwi 14:19
Benny: Gratuluję!

2 kwi 14:20
Eta:

2 kwi 14:33
Benny: Zad 5
7
√log73=a
log
37
√log73=log
3a
√log73*log
37=log
3a
√log37=log
3a
3
√log37=b
log
33
√log37=log
3b
√log37=log
3b
log
3b=log
3a
a=b
2 kwi 14:34
Eta:
ok

można też tak: 7
√log73 =3
√log37 /
√log37 ⇒ 7=7
2 kwi 14:39
Benny: Hmm a to 4?
zad 4
n=3k lub n=3k+1 lub n=3k+2
n
2=9k
2 lub n
2=9k
2+6k+1 lub n
2=9k
2+12k+4
n
2=3k*3k lub n
2=3k(3k+2)+1 lub n
2=3(k
2+4k+1)+1
Nie za bardzo wiedziałem jak to zapisać to spróbowałem tak i coś tam niby wyszło. Mam nadzieję,
że chociaż trochę dobrze

2 kwi 14:57
Eta:
@
Benny
Dobrze i nie za bardzo dobrze
Musisz pisać komentarze( a tu ich brak) ,to konieczne!
4/ Komentarz: każdą liczbę naturalną n możemy zawsze zapisać w postaci:
n= 2a v n=2a+1
n= 3a v n= 3a+1 v n=3a+2
:
n= 6a v n=6a+1 v n=6a+2 v n=6a+3 v n=6a+4 v n=6a+5
gdzie n,a∊N
itd...........
dla n=3a ⇒ n
2= 9a
2= 3*(3a
2)= 3*k , gdzie k=3a
2 i k∊N
n=3a+1 ⇒n
2= ...........=3*(3a
2+2a)+1 =3k+1 ,k= 3a
2+2a
n=3a+2 ⇒ ......... dokończ.......
zatem kwadrat każdej liczby naturalnej można przedstawić w postaci
3k lub 3k+1 , k∊N
c.n.w

2 kwi 16:39
Benny: ale tak można wypisywać w nieskończoność
n=3a+2
n2=9a2+6a+4=3(3a2+2a+1)+1=3k+1, k=3a2+2a+1
czemu coś mi nie pasuje dla n=4a np?
16a2 jak zapisać?
2 kwi 17:00
Mila:
Wystarczy wykazać, że :
Kwadrat liczby naturalnej przy dzieleniu przez 3 daje resztę 0 lub 1.
Warto zapamiętać.
2 kwi 17:12
Benny: Więc wystarczy tylko wykazać dla n=3k, n=3k+1 i n=3k+2?
2 kwi 17:13
Eta: 
2 kwi 17:19
Eta:
W zadaniu mamy wykazać 3k v 3k+1
dlatego bierzemy liczby postaci :n=3a i n=3a+1 i n=3a+2
2 kwi 17:22
Benny: Czyli do mojego rozwiązania brak komentarza tylko?
2 kwi 17:30
Eta:
tak
2 kwi 17:55
Benny: Dziękuję

2 kwi 17:57
Benny: Coś nowego się znajdzie?

2 kwi 20:16
Mila:
Do moich zadań załóż nowy wątek.
2 kwi 20:29
2 kwi 20:36






 Wychowawczyni(od matmy) mówiła, żebym kombinował coś z
matmą stosowaną, myślałem o tym, ale co można po tym robić? Co tu robić?
Wychowawczyni(od matmy) mówiła, żebym kombinował coś z
matmą stosowaną, myślałem o tym, ale co można po tym robić? Co tu robić?
 wszystko
wszystko  studia są po to by udowodnić pracodawcom, że
umiesz się SAM zorganizować , nauczyć i dobrze wykonać zadania
studia są po to by udowodnić pracodawcom, że
umiesz się SAM zorganizować , nauczyć i dobrze wykonać zadania 

 będzie dużo łatwiej
będzie dużo łatwiej  w obecnej erze informatycznej i tak pracę zmienisz kilkanaście razy z kierunek działań pewnie
ze 3 więc najważniejsza jest elastyczność i umiejętność dostosowania do zmian i szybkiej
organizacji się w nowym miejscu (czyli to co masz na każdych studiach )
w obecnej erze informatycznej i tak pracę zmienisz kilkanaście razy z kierunek działań pewnie
ze 3 więc najważniejsza jest elastyczność i umiejętność dostosowania do zmian i szybkiej
organizacji się w nowym miejscu (czyli to co masz na każdych studiach )

 1) x∊(−∞;−8>∪<−5;4>
2)
|Ω|=64
tutaj będą takie możliwości:
(1,2,5,6)−>4!
(1,3,4,5)−>4!
1) x∊(−∞;−8>∪<−5;4>
2)
|Ω|=64
tutaj będą takie możliwości:
(1,2,5,6)−>4!
(1,3,4,5)−>4!

 między czerwoną a niebieską linią jest kąt α
x2=H2+(2h)2
a2+H2=y2
x2=y2+d2−2dycosα
2h=a√3
między czerwoną a niebieską linią jest kąt α
x2=H2+(2h)2
a2+H2=y2
x2=y2+d2−2dycosα
2h=a√3










 f(x)=3 dla x∊<1,2> lub x∊<4,5>
Dla m=3 istnieje nieskończenie wiele rozwiązań.
f(x)=3 dla x∊<1,2> lub x∊<4,5>
Dla m=3 istnieje nieskończenie wiele rozwiązań.



 maturka, zadanie z optymalizacji −1 pkt za brak oznaczeń, prawdopodobieństwo −2(całość)
pomyliłem kolory, −3 pkt dowód, który był prosty, ale nie wpadłem na pomysł i −1 pkt za
udowodnienie, że liczba jest podzielna przez 16.
Otrzymałem takie wyrażenie 8*(n+1)(n2+2n+2) i napisałem, że dla n nieparzystych n+1 jest
podzielne przez 2, a dla n parzystych n2+2n+2 jest podzielne przez 2 a powinienem napisać że
jeśli jest parzysta to n=2k a jak jest nieparzysta to n=2k+1. Czemu za mój sposób nie
otrzymałem pkt?
Co do Twojego zadanka to otrzymałem trzy ciągi:
maturka, zadanie z optymalizacji −1 pkt za brak oznaczeń, prawdopodobieństwo −2(całość)
pomyliłem kolory, −3 pkt dowód, który był prosty, ale nie wpadłem na pomysł i −1 pkt za
udowodnienie, że liczba jest podzielna przez 16.
Otrzymałem takie wyrażenie 8*(n+1)(n2+2n+2) i napisałem, że dla n nieparzystych n+1 jest
podzielne przez 2, a dla n parzystych n2+2n+2 jest podzielne przez 2 a powinienem napisać że
jeśli jest parzysta to n=2k a jak jest nieparzysta to n=2k+1. Czemu za mój sposób nie
otrzymałem pkt?
Co do Twojego zadanka to otrzymałem trzy ciągi:


 3n(n2+2) = 3n[(n2−1)+3] = .........
3n(n2+2) = 3n[(n2−1)+3] = .........
 więc mamy:
2)
3n[(n−1)(n+1)+3]=3n(n−1)(n+1)+9n
9n na pewno dzieli się przez 9, a 3n(n−1)(n+1) też dzieli się przez 9, ponieważ wśród 3
kolejnych liczb naturalnych jedna jest podzielna przez 3
więc mamy:
2)
3n[(n−1)(n+1)+3]=3n(n−1)(n+1)+9n
9n na pewno dzieli się przez 9, a 3n(n−1)(n+1) też dzieli się przez 9, ponieważ wśród 3
kolejnych liczb naturalnych jedna jest podzielna przez 3  Dzięki temu znalazłem analogie do 3
Dzięki temu znalazłem analogie do 3  3)
n(n−1)(n+1)(n2+1)=n(n−1)(n+1)[(n2−4)+5]=n(n−1)(n+1)(n+2)(n−2)+5n(n−1)(n+1)
n(n−1)(n+1)(n+2)(n−2) to wyrażenie dzieli się przez 30, ponieważ jest to 5 kolejnych liczb
naturalnych, więc jedna na pewno dzieli się przez 2,3,5
5n(n−1)(n+1) to wyrażenie dzieli się przez 30, ponieważ są tu 3 kolejne liczby naturalne z
których jedna na pewno dzieli się przez 2 i przez 3
3)
n(n−1)(n+1)(n2+1)=n(n−1)(n+1)[(n2−4)+5]=n(n−1)(n+1)(n+2)(n−2)+5n(n−1)(n+1)
n(n−1)(n+1)(n+2)(n−2) to wyrażenie dzieli się przez 30, ponieważ jest to 5 kolejnych liczb
naturalnych, więc jedna na pewno dzieli się przez 2,3,5
5n(n−1)(n+1) to wyrażenie dzieli się przez 30, ponieważ są tu 3 kolejne liczby naturalne z
których jedna na pewno dzieli się przez 2 i przez 3




 znasz takie?
znasz takie?



 Ładne zadanka Eto.
Ładne zadanka Eto.



 Pozdrawiam
Pozdrawiam 
 Poza tym obowiazuje ustawa o bezstresowym wychowaniu
Poza tym obowiazuje ustawa o bezstresowym wychowaniu 
 2log35−5log32
2log35=a
5log32=b
log32log35=log3a
log35*log32=log3a
log35log32=log3b
log32*log35=log3b
log3b=log3a
a=b
a−b=a−a=0
Zadanko 3
nie mam już chyba pomysłów, wyłączanie, jakieś dziwne kombinowanie, skończyłem na
przedstawieniu tych liczb za pomocą sumy ciągu
2log35−5log32
2log35=a
5log32=b
log32log35=log3a
log35*log32=log3a
log35log32=log3b
log32*log35=log3b
log3b=log3a
a=b
a−b=a−a=0
Zadanko 3
nie mam już chyba pomysłów, wyłączanie, jakieś dziwne kombinowanie, skończyłem na
przedstawieniu tych liczb za pomocą sumy ciągu 
 A jak rozwiązywałeś zad.2/ ?
to 3/ identycznie
A jak rozwiązywałeś zad.2/ ?
to 3/ identycznie 
 Liczba 77775 kończy się 7, liczba 4444 kończy się 6 a liczba 3321 kończy się 3 więc 7+6−3=10
liczba 77775+4444−3321 kończy się cyfrą 0 więc dzieli się przez 10
Liczba 77775 kończy się 7, liczba 4444 kończy się 6 a liczba 3321 kończy się 3 więc 7+6−3=10
liczba 77775+4444−3321 kończy się cyfrą 0 więc dzieli się przez 10



 można też tak :
(n+1)(n+4)(n+2)(n+3)+1= (n2+5n+4)*[(n2+5n+4)+2]+1= .........
można też tak :
(n+1)(n+4)(n+2)(n+3)+1= (n2+5n+4)*[(n2+5n+4)+2]+1= .........








 można też tak: 7√log73 =3√log37 /√log37 ⇒ 7=7
można też tak: 7√log73 =3√log37 /√log37 ⇒ 7=7




