hard Archy: w ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość a. Kąt między krawędzią boczną i podstawą jest równy kątowi płaskiemu przy wierzchołku ostrosłupa.Oblicz objętośc tego ostrosłupa.

Mila: Masz odpowiedź, to napisz.

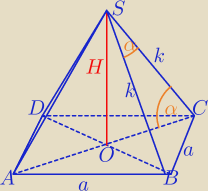
Mila: W ΔBCS: a²=k²+k²−2k*k cosα a²=2k²−2k² *cosα a²=k²*(2−2cosα)

	a2
(1) k2=
	2−2cosα

	a√2
W ΔSOC: |OC|=
	2

	12a√2
cosα=		⇔
	k

	a√2
k=
	2cosα

==========

	a2
(2) k2=
	2cos2α

Z (1) i (2)

a2		a2
	=		⇔
2−2cosα		2cos2α

2cos²α=2−2cosα cos²α+cosα−1=0 cosα=t, t∊(0,1) , α− kąt ostry t²+t−1=0 Δ=1+4=5

	−1−√5		−1+√5
t=		∉D lub t=
	2		2

	−1+√5
cosα=
	2

	a√2
k=
	√5−1

============ W ΔSOC:

	a√2
H2=k2−(		)2
	2

Spróbujesz dokończyć? Licz objętość sam.

Archy: nie mam odpowiedzi.. ok spróbuję

Archy:

	2a2		2a
czyli H=√		−
	1+√5		4

Archy:

	1
więc pole to		&a2*P{8a2−2a−2a√5}{4+4√5}
	3

czy wynik można zostawić w takiej postaci?

Archy: źle zapisałem

1		8a2−2a−2a√5
	*a2*√
3		4+4√5

Mila:

	a√2		2a2
H2=(		)2−
	(√5−1)		4

	2a2		a2
H2=		−
	5−2√5+1		2

	2		1
H2=a2*(		−		)
	6−2√5		2

	2		1
H2=a2*(		−		)
	2*(3−√5)		2

	2−3+√5
H2=a2*
	2*(3−√5)

	√5−1
H2=a2*
	2*(3−√5)

Usuń niewymierność z mianownika i dokończ

Mila: Po co liczysz pole, masz obliczyc objętość.

	(√5−1)*(3+√5)
H2=a2*
	2*(9−5)

	√5+1
H2=a2*
	4

	a√√5+1
H=
	2

	1		a√√5+1
V=		*a2*
	3		2

	a3*√√5+1
V=
	6

Archy: dzięki

Mila: