styczna do wykresu funkcji w punkcie vdmath: Proszę o pomoc w rozwiązaniu zadania:

	x3
Funkcja f określona wzorem f(x)=		dla x≠1. Prosta o równaniu x=−2 przecina wykres
	x+1

funkcji f w punkcie P. Znajdź równanie stycznej do wykresu funkcji f w punkcie P.

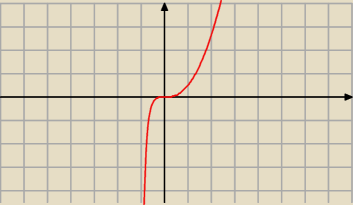
5-latek: To jest wykres tej funkcji Skoro asymtota pionowa to x=−1 to x=−2 nie bedzie przecinac tego wykresu Ale prosta x=2 juz przecina

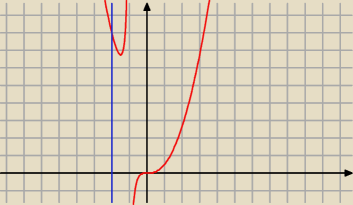
ICSP: a to jest wykres funkcji w troszkę mniejszej skali. Jak widać na tym rysunku prosta x = −2 przecina już wykres funkcji f

5-latek: Czesc ICSP Jak to rozdzielczosc wplywa na wynik Dawniej bym go robil na papierze milimetrowym

ICSP: Wzór na styczną w punkcie x₀ : y − f(x₀) = f'(x₀)(x − x₀) Wystarczy podstawić do wzoru.

vdmath: Zakładając, że jest w takim razie błąd w zadaniu i przyjmując, że prosta ma równanie x=2, to jak to rozwiązać?

vdmath:

	3x2
f'(x0)=
	2

f'(−2)=6 f(−2)=8 P(−2,8) y=6(x+2)+8=6x+20 niestety w odpowiedziach jest y=−4x, dlatego proszę o pomoc

5-latek: Ale w poscie 10:50 widzisz ze przecina go (po zmniejszseniu rozdzielczosci Masz przeciez napisany wzor to licz

	(−2)3
f(−2)=		=.......
	−2+1

f'(x)= policz potem policz pochodna dla x=−2 Wstawiaj dane do wzoru i final

vdmath: policzyłam dla −2 f(−2)=8 f'(−2)=6 wstawiłam do wzoru i wyszło 6x+20, a nie jak w odpowiedziach y=−4x

5-latek: https://matematykaszkolna.pl/strona/359.html 2 wzor od doolu do obliczenia pochodnej

vdmath:

	x2(x+3)
czyli f'(x)=
	(x+1)2

f'(−2)=4 y=4x+16 i nadal nie co jeszcze robię źle?

5-latek: Zle liczysz pochodna

vdmath:

	x2(2x+3)
f'(x)=
	(x+1)2

vdmath: Eureka. Wyszło Dzięki wielkie. Jeszcze muszę posiedzieć nad pochodnymi

5-latek:

	2x3+3x2
=
	(x+1)2

teraz licz f'(−2)

5-latek: