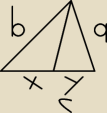 Zadanie mam następujące: Odcinek padający na bok c jest dwusieczną. Wyraź jego długość za
pomocą a,b,c
Z twierdzenia steinera i o dwusiecznej wyszło mi (oznaczmy szukaną jako d, i załóżmy że d
dzieli c na odcinki x i y) że d=√ab−xy
mógłby ktoś pomóc, jak wyrazić xy za pomocą a, b, c?
Zadanie mam następujące: Odcinek padający na bok c jest dwusieczną. Wyraź jego długość za
pomocą a,b,c
Z twierdzenia steinera i o dwusiecznej wyszło mi (oznaczmy szukaną jako d, i załóżmy że d
dzieli c na odcinki x i y) że d=√ab−xy
mógłby ktoś pomóc, jak wyrazić xy za pomocą a, b, c?
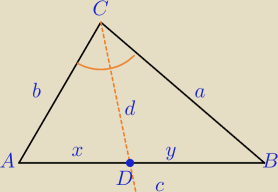 a*b=d2+x*y
d2=ab−x*y
Z tw. o dwusiecznej kąta :
a*b=d2+x*y
d2=ab−x*y
Z tw. o dwusiecznej kąta :
| b | x | ||
= | ⇔ | ||
| a | y |
| b | x | |||
(1) | = | |||
| a | c−x |
| b*c | ||
x= | ||
| a+b |
| b | c−y | |||
(2) | = | stąd | ||
| a | y |
| a*c | ||
y= | ||
| a+b |
| b*c | a*c | |||
d2=a*b− | * | ⇔ | ||
| a+b | a+b |
| abc2 | ||
d2=a*b− | ||
| (a+b)2 |
| ab*(a+b)2−abc2 | ||
d2= | ||
| (a+b)2 |
| ab*[(a+b)2−c2] | ||
d2= | ||
| (a+b)2 |
| ab*(a+b+c)*(a+b−c) | ||
d2= | ||
| (a+b)2 |
| √ab*(a+b+c)*(a+b−c) | ||
d= | ||
| a+b |
| 2ab | a2+b2−c2 | |||
⇒ bd+ad=2abcosγ ⇔ (*)d= | cosγ, ale cos2γ= | ⇔ | ||
| a+b | 2ab |
| a2+b2−c2 | (a+b)2−c2 | |||
⇔ 1+cos2γ= 1+ | ⇔ 2cos2γ= | ⇔ | ||
| 2ab | 2ab |
| (a+b−c)(a+b+c) | ||
⇔ cos2γ= | i 0<γ<12π ⇒ | |
| 4ab |