planimetria
xx2: Dany jest trójkąt ABC, w którym |BC|=a, |AC|=b oraz miara kąta ACB = 120 stopni. Punkt D jest
środkiem boku AB tego trójkąta. Udowodnij, że |CD| =
12√a2 − ab + b2.
Wyznaczyłem z tw. cosinusów bok leżący naprzeciwko kąta ACB i nie wiem co dalej. Byłbym
wdzięczny jakby mi ktoś pomógł

20 mar 14:47
stonoga: | | 1 | |
czy tam nie powinno być, udowodnij że |AD| lub |BD| = |
| √a2 − ab + b2 |
| | 2 | |
20 mar 15:14
xx2: Nie. Chodzi o środkową |CD|.
20 mar 15:20
Jaro: Poczytaj sobie o twierdzeniu Stewarta. Z niego się dowiesz (podstawiając do wartości w tym
zadaniu, przyjmijmy na razie, że |AB|=c), że:
| | 12a2c+12b2c | |
|CD|2= |
| −(12c)2 (1) |
| | c | |
c, jak pewnie wyliczyłeś z twierdzenia cosinusów, jest równe
√a2+b2−2absin(120)=
√a2+b2−ab (2)
podstawiamy (2) do (1), skracając wcześniej c:
| | 1 | | 1 | |
|CD|2= |
| (a2+b2)− |
| (a2+b2−ab) |
| | 2 | | 4 | |
Koniec. Wystarczy, że sprowadzisz do wspólnego mianownika, uprościsz co się da i wychodzi, że
|CD|=
√14(a2−ab+b2)
pozdrawiam
20 mar 15:41
prosta:
a
2=x
2+c
2−2cxcosα
b
2=x
2+c
2+2cxcosα
a
2+b
2=2x
2+2c
2
| | a2+b2−2abcos120o | |
a2+b2=2x2+2 |
| |
| | 4 | |
4x
2=a
2+b
2−ab
20 mar 16:21
stonoga:
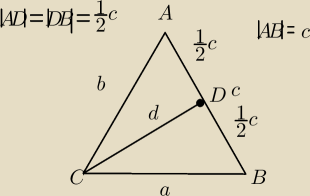
kąt ACB = 120
o, kąt CDB = α, a kąt CDA = 180
o − α
korzystamy z twierdzenia cosinusów najpierw dla trójkąta ABC
c
2=a
2+b
2−2ab−cos120
o
| | 1 | |
c2=a2+b2+ab (cos120o = − |
| ) |
| | 2 | |
c =
√a2+b2+ab =
√(a+b)2
teraz korzystamy z twierdzenia cosinusów dla trójkątów ACD i DCB
| | 1 | |
a2 = d2 + ( |
| c)2 − 2ab cosα |
| | 2 | |
| | 1 | |
b2 = d2 + ( |
| c)2 − 2ab cos(180o−α) |
| | 2 | |
cos(180
o−α) = −cosα
| | 1 | |
a2 = d2 + |
| c2 − 2ab cosα |
| | 4 | |
| | 1 | |
b2 = d2 + |
| c2 + 2ab cosα |
| | 4 | |
dodajemy stronami
| | 1 | | 1 | |
d2= |
| (a2 + b2 − |
| c2) |
| | 2 | | 2 | |
za c podstawiamy
√(a+b)2
| | 1 | | 1 | | 1 | |
d= |
| √2a2+2b2−(a+b)2= |
| √2a2+2b2−a2−ab−b2= |
| √a2+b2−ab |
| | 2 | | 2 | | 2 | |
20 mar 17:24

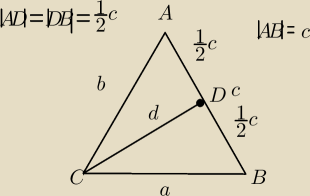 kąt ACB = 120o, kąt CDB = α, a kąt CDA = 180o − α
korzystamy z twierdzenia cosinusów najpierw dla trójkąta ABC
c2=a2+b2−2ab−cos120o
kąt ACB = 120o, kąt CDB = α, a kąt CDA = 180o − α
korzystamy z twierdzenia cosinusów najpierw dla trójkąta ABC
c2=a2+b2−2ab−cos120o