Symetralna odcinka Daniel: Wyznacz rownanie symetralnej odcinka AB A=(1,2) B=(3,−2) Wyznaczylem juz srodek odcinka jest to (2,0), dobrze zrobilem? I teraz co dalej mam zrobic? Prosilbym o pomoc

Janek191: Tak. Wyznacz równanie prostej AB , a następnie prostej prostopadłej do pr AB przechodzącej przez S = ( 2 , 0)

Mila: Napisać równanie prostopadłej do prostej AB ( wystarczy znać jej wsp. kierunkowy) i przechodzącej przez punkt S=(2,0).

Daniel: Hmm, za duzo mi to nie mowi, jakas podpowiedz?

Mila: Umiesz napisać równanie prostej przechodzącej przez dwa różne punkty?

Daniel: To jest ten wzor tak? (x2−x1)(y−y1)=(y2−y1)(x−x1) i po prostu do tego podstawic A i B i to obliczyc?

5-latek: Pytanie nr 1. Co to jest symetralna odcinka ? . czekam na odpowiedz

Daniel: Dobra obliczylem to z tego wzoru i mi wyszla prosta y=−2x+4 no a symetralna to jest prosta prostopadła do odcinka i przechodząca przez jego srodek

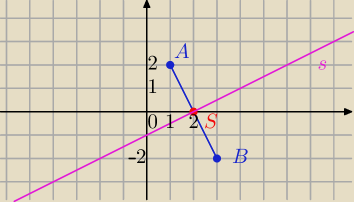
Mila: y=ax+b równanie kierunkowe prostej A=(1,2) B=(3,−2) współrzędne tych punktów spełniają równanie prostej⇔ 2=a*1+b −2=a*3+b =========odejmuję stronami 4=−2a a=−2 AB: y=−2x +b prosta prostopadła do AB ma wsp. kierunkowy (a' ) taki, że (−2)*a'=−1⇔

	1
a'=
	2

	1
s: y=		x+b i symetralna przechodzi przez S=(2,0)⇔
	2

	1
0=		*2+b⇔
	2

0=1+b b=−1

	1
s: y=		x−1
	2

5-latek:

	−2−2		4
wspolczynnik a prosytej AB=		= −		=−2 wiec twoje rownanie jest zle
	3−1		2

Daniel: Aha o to chodzi, dzieki Mila Teraz mam 2 zadanko Sprawdz czy punkty P M L leza na jednej prostej (czy sa wspołliniowe) P= (2 ,0) M= (0,−1) L= (4, 2) Mam tu wziasc np punkty PM i obliczyc prosta z tego wzoru (x2−x1)(y−y1)=(y2−y1)(x−x1)?

Mila: Tak, a potem sprawdzić, czy wsp. punktu L spełniaja to równanie. Narysuj w układzie wsp.

Daniel: Prosta wyjdzie y= 1/2x−1 ?i jak sprawdzic czy wsp punktu l spelaniaja to rownanie?

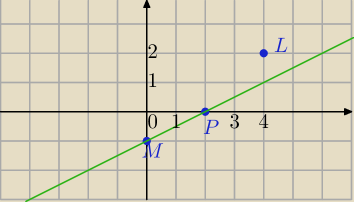
Mila: Podstawić do równania ,

	1
y=		*4−1=2−1=1≠2⇔L∉prostej MP⇔punkty nie są współliniowe.
	2

albo graficznie, tu wyraźnie widać, że L∉prostej MP

Daniel: I to jest koniec zadania tak? jeszcze mam takie jedno, ale nie wiem o co tam chodzi Wykaz, ze trojkat PQR jest prostokatny i oblicz jego obwod P =(−4 −6) Q=(2,5) R=(−2,4)

Daniel: To jest moje ostatnie zadanko, dzieki Twojej pomocy Mila te zadania wyzej juz ogarnalem... bo jutro poprawiam sprawdzian i bedzie wlasnie takie zadanie, jakie podalem

5-latek: To narysuj te punkty na ukladzie wspolrzdnych Teraz jaki warunek musza spelniac boki aby trojkat byl prostokatny ? albo jaki warunek musi spelniac iloczyn skalarny aby kat miedzy wektorami wynosil 90 stopni ? Obwod −−masz wzor na dlugosc odcinka wiec policz dlugosci i dodaj

Daniel: Wyzsza szkola jazdy =D

Mila: c²=a²+b² to coś Ci przypomina?

Daniel: No tak, twierdzenie pitagorasa

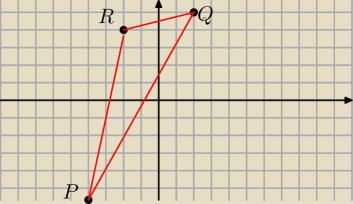
5-latek: Jesli trojkat ma byc prostokatny to z twierdzenia pitagorasa |PQ|²= |RQ|²+|PR|² (z rysunku wida z e PQ jest najwiekszym bokiem gdzie |a| −oznacza dlugosc odcinka np |PQ| to dlugosc odcinka PQ https://matematykaszkolna.pl/strona/1248.html to jest wzor na dlugosc odcinka wiec policz dlugosci bokw |PQ| |PR| I |RQ| dodaj do siebie te dlugosci i masz obwod Potem spawdz z tego czy ten trojkat jest prodstokatny

Daniel: PQ wyszlo mi pierwiastek z 157

Mila: Dobrze.

Daniel: PR pierwiastek z 104 QR pierwiastek z 17 dobrze? ;s

5-latek: Najlepiej jakbys pisal obliczenia

Daniel: PR=(−2+4)²+(4+6)²=2²+10²=4+100=104 QR=(−2−2)²+(4−5)²=(−4)²+(−1)²=16+1=17 Oczywiscie wszystko pod pierwiastkiem