planimetria Michał: Witam, Czy mogę sobie zadanie z planimetrii przenieść do układu współrzędnych? Wpadłem na pewne rozwiązanie nie wiem czy dobre, ale bardzo proste, także bardzo prawdopodobne i nie wiem czy mogę je wklepać w układ. Za odpowiedzi dziękuję

Mila: Możesz. Napisz to zadanie.

Michał:

	|AK|		1
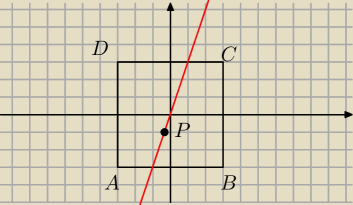
Przez środek kwadratu ABCD i punkt K na boku AB taki, że		=		przechodzi
	|KB|		2

prosta. Na odcinku tej prostej, wewnątrz kwadratu, wybieramy dowolny punkt P. Udowodnij, że odległości punktu P od boków AB, AD, BC, CD tworzą w podanej kolejności ciąg arytmetyczny. Ale to chyba nie o to chodzi. Bo nie wychodzi mi żaden ciąg arytmetyczny :< A=(−a,−a) B=(a,−a) C=(a,a) D=(−a,a) y=3x P=(x,3x) i teraz wzorami z tablic maturalnych odległość prostej od punktu. AB: y=−a BC: x=a CD: y=a AD: x=−a i odległości: d(AB,P)=|3x+a| d(BC,P)=|x−a| d(CD,P)=|3x−a| d(AD,P)=|x+a| I niestety nic nie uzyskałem ciekawego :< chyba, że gdzieś jest pomyłka.

Michał: punktu K nie wbiłem w układ

Michał: https://matematykaszkolna.pl/forum/268427.html Znalazłem zadanie, które robił Tadeusz, ale trochę nie mam pojęcia jak mu to wyszło. Na razie jestem dumny z pomysłu z układem

Mila: https://matematykaszkolna.pl/forum/268427.html

PW:

	a		a
Założyliśmy, że a > 0. Z warunków zadania wynika, że x∊(−		,		). Rozpatrz osobno
	3		3

	a		a
x∊(−		, 0) lub x∊[0,		).
	3		3

Prawdę mówiąc z uwagi na symetrię wystarczy wziąć ten drugi przedział. Pozbędziesz się wtedy wartości bezwzględnych i będzie widać. Sposób poprawny, wprowadzenie układu współrzędnych powala uniknąć obliczania odległości "poprzez jakieś trójkąciki".

Michał: W takim razie wychodzi to tak(rozpatrze tytlko jeden przedział)

	a
x∊<0,		>
	3

d(AB,P)=|3x+a|∊<a,2a>

	4a
d(AD,P)=|x+a|∊<a,		>
	3

	2a
d(BC,P)=|x−a| ∊<−a,−		>
	3

d(CD,P)=|3x−a|∊<−a,0> Nadal nic nie widzę niestety w tym

Michał: źle, zapomniałem o wartościach bezwzględnych... ale i tak nic z tego mi nie wychodzi

PW: 3x < a, a więc np. |3x − a| = a − 3x − masz opuścić moduły, że się tak niefachowo wyrażę. Potem badać różnice między kolejnymi wyrazami (bo tak się bada, czy ciąg jest arytmetyczny).

Michał: aaaaaaa, przepraszam. inaczej sobie wyobrażałem rozwiązanie po prostu Nie podaję odpowiedzi, bo wszystko jest, a jakby ktoś miał podobny problem to nie przepisze bezmyślnie, tylko chociaz trochę bedzie musiał pomyśleć PW − dzięki!