Planimetria Blue: Mam kilka zadań z planimetrii, których nie umiem zrobić: zad.3 W trójkącie równoramiennym ABC: |AC|= |BC| i punkt D jest środkiem boku AC. Na przedłużeniu boku AB wybrano punkt E. Oznaczmy |BE|= n*|AB|, n>0 (patrz rysunek). Udowodnij,

	n+1
że punkt przecięcia odcinka DE z ramieniem BC dzieli to ramię w stosunku		.
	n

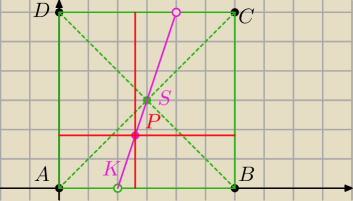
zad.4 Przez środek kwadratu ABCD i punkt K na boku AB taki, że |AK| : |KB| = 1:2 przechodzi prosta. Na odcinku tej prostej, wewnątrz kwadratu, wybieramy dowolny punkt P. Udowodnij, że odległości punktu P od boków AB, AD, BC, CD tworzą w podanej kolejności ciąg arytmetyczny. zad.8 W trójkącie ABC dwa boki i środkowa o końcach w punkcie A mają odpowiednio długości 4,6,√10. Oblicz długość trzeciego boku tego trójkąta. 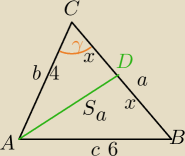zad.9 W trójkącie ABC kąt przy wierzchołku B jest trzy razy większy od kąta przy wierzchołku C. Dwusieczna AD kąta A dzieli trójkąt ABC tak, że pole trójkąta ACD jest dwa razy większe od pola trójkąta ABD. Wyznacz miary kątów trójkąta ABC. 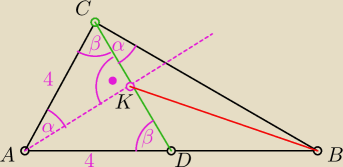zad.12 W trójkącie prostokątnym ABC, w którym kąt przy wierzchołku C jest prosty i |AB| =8, dwusieczna kąta A i środkowa CD przecinają się pod kątem prostym w punkcie K. Wyznacz długość odcinka BK. 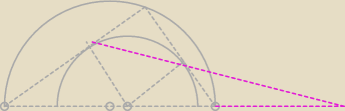zad.13 Dany jest trójkąt prostokątny ABC, w którym kąt przy wierzchołku C jest prosty i |AC|>|BC|. Środek okręgu stycznego do boku BC w punkcie E i do boku AC w punkcie D leży na przeciwprostokątnej i dzieli ją na odcinki o długościach 15 i 20. b) Proste AB i DE przecinają się w punkcie P. Oblicz długości odcinków PB i PE. Skan do zadania 3: http://i60.tinypic.com/1eq72o.jpg Bardzo proszę o pomoc w rozwiązaniu

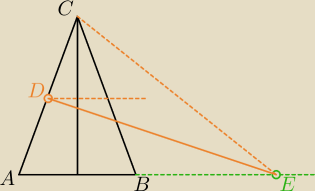
Tadeusz: ... a podobieństwo trójkątów widzisz?

Kacper: Pomyślimy

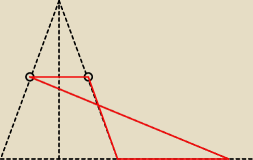
Tadeusz: ... teraz już chyba wiadomo −

Mila: 8) Jeżeli masz w tablicach wzór na środkową, to korzystasz i zadanie proste.

	1
Sa=		√2b2+2c2−a2
	2

S_a=√10

	1
√10=		*√2*42+2*62−a2 /*2
	2

2√10=√104−a² /² a²=64 a=8 II sposób Dwa razy korzystasz z tw. cosinusów W ΔADC: (1) (S_a)²=4²+x²−2*4*x cosγ W ΔABC: 6²=4²+(2x)²−2*6*2x*cosγ obliczas cosγ w zależności od (x) i podstawiasz do (1) i obliczasz x a=2x ====

Mila: Znalazłaś może odpowiedzi do ostatniej matury R?

Blue: Mila, mówisz o Operonie Dzięki, zaraz będę analizować te zadanka.. Ogólnie rozwiązałam właśnie maturkę z Operonu i muszę Wam powiedzieć, że jest dobrze Ale beka z tym zadaniem z graniastosłupem , gdzie się pomylili ^^

Mila: Tak. Operon R.

Blue: No to oczywiście, że znalazłam, przecież są na stronie Ale przyznaj, że 1000 razy prostsza od WSiPu Milu, czy mogłabyś tutaj zajrzeć: https://matematykaszkolna.pl/forum/268487.html

Mila: Podaj mi linka do tej strony, bo chcę wydrukować dla ucznia.

Blue: http://arkusze.gieldamaturalna.pl/?utm_source=operon.pl&utm_medium=www&utm_campaign=operon.pl%20banner proszę

Blue:

	2n+1
Mi wyszło w tym 3		...
	2n

Mila: Dziękuję za adres. Wydrukuję sobie te arkusze. Trzeciego nie liczyłam, poczekaj na Tadeusza, nie chcę się wtrącać. Jeśli nic nie napisze, to policzę.

Tadeusz: ... już jestem −

	n+1
Wychodzi dokładnie tak jak w odpowiedzi czyli
	n

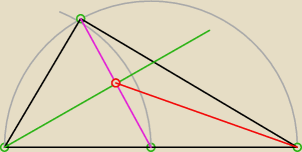
Tadeusz: 12) ... proste −

Tadeusz: .. oczywiście jak już wykażesz. że trójkąt ADC jest równoboczny −

Blue: Tadeusz, proste to pojęcie subiektywne....dla mnie to nie jest proste

Tadeusz: ... masz odpowiedź .... czy to 2√7 ?

Tadeusz:

Tadeusz: ... "bawisz się" czy odpuściłaś na razie ?

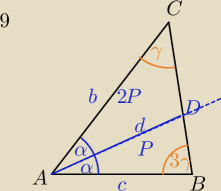
Mila: 9) P_ΔADC=2*P_ΔABD⇔

1		1
	*b*d*sinα=2*		*c*d*sinα⇔
2		2

b=2c Z tw. sinusów w ΔABC:

c		2c
	=		⇔
sin(γ)		sin(3γ)

2sinγ=sin(3γ) sinγ+sinγ−sin(3γ)=0 sinγ+2*cos(2γ)*sin(−γ)=0 Dokończ

Blue: Tadeusz, czyli do 12 z tw. cosinusów?

Blue: Tak, taka jest odpowiedź do zadania 12, teraz już rozumiem

Blue: 8 też rozumiem...

Tadeusz:

Blue:

	1
Mila, w tym 9 będzie tak : sinγ=t, 4t3−t=0 sinγ=		, γ=30, 3γ=90
	2

Tadeusz: masz odpowiedź do 13 ? Wychodzi mi, że PB=45

Mila: A nie mogłaś wyłączyć sinγ?

	π
sinγ*(1−2cos(2γ))=0 i 0<γ<
	3

	1
sinγ=0,γ∉D lub cos(2γ)=
	2

	π
2γ=
	3

	π
γ=
	6

Kąty Δ:

π		π		π
	,		,
6		2		3

Blue: Tadeusz, to jest do 13

Blue: W sumie mogłam, ale jakoś tak rzuciły mi się w oczy wory ^^ Każdy sposób jest dobry

Blue: Tadeusz, tak jest w odpowiedziach

Blue: wzory* haha

Tadeusz: tak ....pytam o odpowiedź do 13)

Tadeusz: ... bardzo ciekawe zadanko ... nie wiem czy jest jakaś prostsza ścieżka ale i ta nie jest bardzo kręta −

Blue: to może byś mi ją przybliżył ?

Blue: bo ogólnie w podpunkcie a do tego zadania było trzeba policzyć promień i z tym sobie poradziłam

Tadeusz: ... mówisz oczywiście o promieniu okręgu wpisanego ?

Tadeusz: .... i wyszedł Ci 12 ?

Blue: tak

Tadeusz: ... jak to policzyłaś to byłaś już "w ogródku" −

Blue: ta to z podobieństwa trójkątów liczyłam

Blue: ja*

Tadeusz: ... ten mój rysunek troszkę zniekształca ...bo nie wpisywał się w pole rysowania Grunt to zauważyć,że wszystkie te trójkąty prostokątne mają boki w proporcji 5:4:3

Blue: tylko Tadeusz, ja nadal nie wiem, jak obliczyć ten podpunkt b)

Tadeusz: ... żartujesz sobie ? −

Blue: Nie...

Tadeusz: ... jeśli na tych moich bazgrołach środek okręgu wpisanego zaznaczysz jako O to bawisz się Taleskiem OD=12 BE= 9 OB=15 OP=15+x gdzie x= szukane BP

12		9
	=		⇒ x=...
15+x		x

Tadeusz: a to zad.3) ...doliczyłaś się? −

Mila: Macie już 13? 45, 36√2 ?

Blue: ahaaa, więc to takie proste xD Dzięki, zaraz wrócę do 3−ciego

Tadeusz: ...Mila ...45 jest OK ....ale 36√2 ....to nie ta bajka −

Tadeusz: ...przepraszam ... może pasować .... nie liczyłem dalej −:(

Blue: tak jest Mila

Blue: Właśnie że ta bajka ^^

Blue: Tadeusz, wyszło mi już 3

Blue: Teraz pozostaje tylko 4

Tadeusz: 4) mam rozwiązane ...ale dziś już nie dam rady wpisać bo muszę zmykać. Jak nie zrobisz ....to wpiszę jutro − Na razie papatki −

Blue: papa Będę czekać jutro, chyba, że coś mnie olśni, ale wątpię

Tadeusz: ...słowo się rzekło ... − Umieszczam ten kwadrat w I ćwiartce układu współrzędnych tak aby wierzchołek A znajdował się w początku układu. Dlaczego tak? ... bo jestem leniwy i nie chcę potem bawić modułami itp. − Jeśli bok kwadratu oznaczę jako a to S=(a/2, a/2) K=(a/3, 0) Prosta przez punkty S i K opisana jest równaniem y=3x−a Punkt P należy do tej prostej zatem P=(x_p, y_p) czyli P=(x_p, 3x_p−a) Wyznaczamy teraz odległości punktu P od: AB to: y_p czyli 3x_p−a AD to: x_p x_p−(3x_p−a)=a−2x_p BC to: a−x_p a−x_p−x_p=a−2x_p CD to a−y_p 2a−3x_p 2a−3x_p−a+x_p=a−2x_p jak widzisz spełniony jest warunek postępu arytmetycznego ... cnu...−

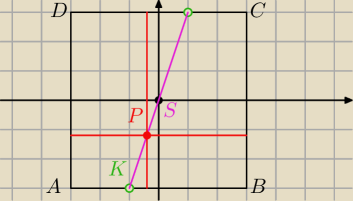
Tadeusz: 1. ... jak widać różnica tego ciągu wyrażona jest poprzez odległość punktu od środka kwadratu. Dla x_p=a/2 ... punkt P pokrywa się ze środkiem S ... ciąg jest stały. 2. Ty jesteś pracowita więc możesz inaczej. Umieść kwadrat tak aby to jego środek pokrywał się z początkiem układu współrzędnych. Wtedy prosta określona jest równaniem y=3x Punkt P=(x_p, 3x_p) ... itd ...też fajna zabawa −

Blue: Dzięki Tadeusz, w życiu bym na to nie wpadła

Tadeusz: ... to ćwicz MŁODA ...ćwicz −

Blue: ok