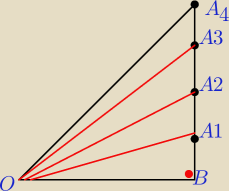
Trygomometria 5-latek: Niech na rysunku bedzie ∡BOA₁=∡A₁OA₂=∡A₂OA₃=∡A₃OA₄=x Opierac sie wlasnosciach dwusiecznej w trojkacie zbadac ktora z liczb jest wieksza tg2x czy 2tgx tg3x czy 3tgx tg3x czy tg2x+tgx Czy wobec tego tangens rosnie proporcjonalnie do kąta ?

Braun: Podstaw jakieś liczby to się przekonasz.

Qulka: https://matematykaszkolna.pl/strona/428.html

Mila:

OB		OA2
	=
BA1		A1A2

	BA1
tgx=
	OB

	BA2
tg(2x)=		=... licz dalej
	OB

5-latek: Witam Musialem wylaczyc komputer bo mi zaszalal Dwusieczna kąta w trojkącie to polprosta ktora dzieli kąt na pol. Wiec np polprosta OA₁ bedzie dwusieczna kąta BOA₂

	2*BA1
Teraz tg(2x)=
	OB

	BA1
a ta 2tgx= 2*
	OB

Teraz nalezy to porownac Aniu wykresy to jeszce daleko to jest dopiero poczatek Powtarzam od zera

5-latek: jak wytlumaczyc ze tg(2x) >2tgx ?

5-latek: Jak wstane to jeszcze dobrze pomysle Dobranoc wszystkim

Qulka: weź kątomierz i popatrz, że albo odcinki nie będą równe albo kąty

5-latek: A wiesz Aniu Mam kątomierz ,ekierki i linijkę Teraz BA₁<A₁A₂ <A₂A₃<A₃A₄ wiec bedzie 2*BA₁<BA₂ takze 3*BA₁<BA₃ i 4*BA₁<BA₄ Teraz bedziemy mieli ze

BA2		2*BA1
	>		czyli tg(2x)>2tgx
OB		OB

BA3		3*BA1
	>		czyli tg(3x)>3tgx
OB		OB

I jeszcze

	BA2		BA1		BA2+BA1		BA3
tg(2x)+tgx=		+		=		<
	OB		OB		OB		OB

Zauwazylem ze tg(nx)>ntgx (dla n>1 i kąta ostrego (bo na razie takie kąty rozpatruje Wiec tangens kąta rosnie szybciej niz kąt

5-latek: Bo tangens kąta jest to stosunek przyprostokatnej lezącej naprzeciw tego kata do drugiej przyprostokątnej lezącej przy tym kącie

5-latek: Zrobilem porzadny rysunek na papierze milimetrowym

Mila: Dobrze zauważyłeś.

5-latek: Bardzo dziekuje