Zadanie Optymalizacyjne
fdsf: Mila , Eta Proszę o pomoc
Na kole o promieniu 4cm opisano trójkąt prostokątny. Wyznacz długości boków tego trójkąta który
ma najmniejsze pole.
mamy uklady rownań:
a+b=c−8
a
2+b
2=c
2
nie mam pojecia jak to rozwiklac
12 mar 00:12
panpawel_v2: wyliczasz z pierwszego c i podstawiasz do 2 pozostałych i masz już tylko 2 zmienne.
12 mar 00:16
fdsf: zrobiłem tak jak mówisz i wychodzi
ab+8a+8b+32=0
i co dalej ?
12 mar 00:23
12 mar 00:23
Qulka: i potem (c+8)2 −8(c+4)=c2
12 mar 00:27
fdsf: c=−4
12 mar 00:30
Qulka: i pole wtedy jest zero
czyli najmniejsze
12 mar 00:32
Janek191::
To będzie Δ prostokątny równoramienny.
12 mar 00:39
Janek191::
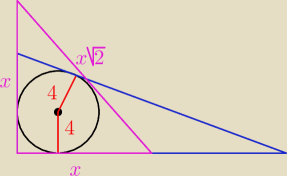
12 mar 00:45
fdsf: Janek rozumiem , ale jak mam do tego dojść i wyliczyć sztywno liczby
12 mar 00:51