matematykaszkolna.pl
Zadanie Optymalizacyjne fdsf: Witam Mam problem z zaczęciem , wyprowadzeniem wzoru na poszczegolne boki trojkata , treść jest następująca: Na kole o promieniu 4cm opisano trójkąt prostokątny. Wyznacz dlugości boków tego trójkąta, który ma najmniejsze pole.
11 mar 14:50
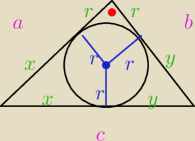
Qulka: rysuneka+b=c+2r= c+8 a2+b2=c2
11 mar 14:59
fdsf: i jak mam wyprowadzic wzor na a lub b ? nie mam pojecia
11 mar 15:54
fdsf: ?
11 mar 18:27
fdsf: pomoże ktoś ?!?!
11 mar 21:26
fdsf: :(
11 mar 22:22
Qulka:
 (a+b+c)r (2c+2r)r 
Pole =
=
= (c+r)r = 4c+16
 2 2 
11 mar 23:51
fdsf: Jeśli mógłbyś mi wyjaśnić co ten wzór na pole nam pomoze jesli i tak mamy wyliczyć b dla a albo a dla b
12 mar 00:28
Qulka: możesz wyliczyć c..to też bok trójkąta emotka ale niestety min osiąga dla c = 0 emotka
12 mar 00:30
fdsf: a powinno byc a=8+4√2 b=a c=8+8√2
12 mar 00:31
Qulka: tradycyjnie równoramienny emotka można naprawdę odpowiadać w ciemno emotka
12 mar 00:33
Qulka: przerzuć się na kąty może emotka
12 mar 00:35
fdsf: ale chyba trzeba dojść do tego że będzie równoramienny z takimi o to długościami boków , mam rozumieć że nie za bardzo orientujesz się jak to rozgryźć ?
12 mar 00:35
Qulka: skoro w tym układzie wszystko nam się skraca do zera trzeba zmienić układ emotka
12 mar 00:41
fdsf: gdybyśmy mieli tylko nowe równania
12 mar 00:45
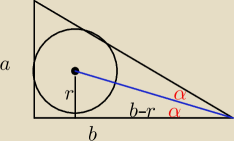
Qulka: rysunek
 4 
tgα=
 b−4 
 a 
tg2α=
 b 
 ab b2tg2α 
P=
=
 2 2 
12 mar 00:55
Qulka:
 4 
b=
+4
 tgα 
 2tgα 
tg2α=
 1−tg2α 
i już mamy tylko α emotka
12 mar 00:57
fdsf: Dalej nie mam pojęcia
12 mar 01:03
Qulka: tgα=u
 16(1+u)2•u 16(1+u) 
P=
=
 u2(1−u2) u(1−u) 
minimum to miejsce zerowe pochodnej
 16(u2+2u−1) 
P'=
=0
 u2(1−u)2 
u= −1+√2 lub −1−√2 dla u=−1+√2 min więc tgα=√2−1 stąd α=π/8 zatem 2α=π/4 = 45°
12 mar 01:59