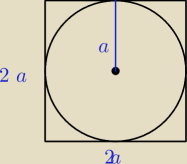
ssd s: W kwadrat wpisano kolo, w kolo zaś trojkat rownoboczny. Obliczyc prawdopodobienstwo, ze losowo wybrany punkt kwadratu jest a) punktem kola b) punktem trojkata Dzięki z góry.

Qulka: Ω=4a² A=πa²

	3a2√3
B=
	4

	π
P(A)=
	4

	3√3
P(B)=
	16

s: czemu Ω 4a² ?

s: ?

Qulka: bo bok kwadratu to 2a, żeby łatwiej potem promień koła, bo będzie a

Jacek: Bo a to promień koła.

s: bok kwadratu to 2a, 2*a*2 = 4a 4a to pole ?

Jacek:

	2a*2a*√3
B=		=a2*√3
	2*2

	√3
P(BA)=
	4

Jacek: Miało być P(B)=√3/4

s: ale czemu tam jest 4a²

s: promień koła to a i dlatego 4a² to pole kwadratu ?

Jacek: A nie dobrze było u Qulki, zaćmienie z mojej strony.

s: punkt koła to również punkt trójkąta ? Dlatego prawdopodobieństwo, że losowy punkt to koło jest większe od prawdopodobieństwa, że losowy punkt to trójkąt ?

s: skąd ta 3 przed a² w polu trójkąta ?

Jacek: Punkt trójkąta to także punkt koła.

s: tak, ale prawdopodobieństwo wylosowanie punktu koła jest większe niż prawdopodobieńśtwo wylosowania punktu trójkąta ?

Qulka: bo bok trójkąta ma długość a√3

s: i dlaczego jest 3 przed a²

s: wzór na bok trójkąta to a√3 ? Czy skąd to się wzieło ?

Jacek: O chyba jednak bok będzie inny, mi wychodzi w głowie 3a/2

Qulka: bo promień okręgu opisanego na trójkącie R=bok √3/3 więc bok trójkąta to R√3 a że R=a więc bok =a√3

s: czemu Ω = 4a² ? a to promień kwadratu, to pole kwadratu = 2a² ?

Qulka: 2a•2a=4a²

s: ok dzięki.

Jacek: Tak, bok trójkąta to √3a. Nie wiedzieć czemu pierwiastkowałem w głowie √12=4. Potem jak z sinusa policzylem to zgadza się z Qulka.

Qulka: aż tak dookoła nie wystarczyło że to 2/3 h oraz h=a√3/2

s: ale czemu tyle bok trójkąta wynosi ? Jak wy go obliczacie ?

Qulka: https://matematykaszkolna.pl/strona/856.html

s:

	√3
h = a
	2

	√3		√3
czyli h = a*a		= a2
	2		2

i jak to dalej wyliczyć, że bok trójkąta to a √3 ?

s:

	√3
h = a
	2

2		√3		a√3
	* a		=		}
3		2		3

jak wy obliczyliście że bok wam wyszedł a√3 ?

Jacek:

	2h
a=		, a w tym przypadku rozumiane jako promień koła opisanego na trójkącie jest w takiej
	3

relacji do wysokości trójkąta (w trójkącie równobocznym)

	√3
h=b*		, b − podstawa trójkąta
	2

	3		2
b=		a*		=√3a
	2		√3

Jacek:

	2
Oczywiście, nie trzeba znać takich relacji, że w równobocznym R (opisanego) =		h ,
	3

da się do tego samemu dojść.

s:

	2h
skąd wziąłeś, że a =		?
	3

s: mógłbyś tak rozpisać od A do Z jak to wyliczaliście ? Bo nie mogę tego zrozumieć

Jacek: 2a, − bok kwadratu Promień koła wpisanego w kwadrat = a b − bok trójkąta równobocznego wpisanego w koło o promieniu a h − wysokość trójkąta równobocznego wpisnego w koło o promieniu a Jest relacja pomiędzy wysokością trójkąta równobocznego wpisanego w okrąg:

	2h
a=
	3

Możesz sobie ją pewnie na kilka sposobów udowodnić. W trójkącie równobocznym stosunek wysokości do boku tego trójkąta to:

	√3
h=b
	2

	3
Pod h podstawiasz		a.
	2

3		√3
	a=b
2		2

, zatem:

	3
b=		a=√3a
	√3

s:

	3
czemu pod h podstawiasz		a ?
	2