proszę o rozwiązanie Michał: Podstawą ostrosłupa jest prostokąt ABCD Krawędż boczna DS jest prostopadła do płaszczyzny podstawy i ma długość H Ściana ABS nachylona do płaszczyzny pod kątem o mierze 45⁰ a ściana BCS pod kątem o mierze 30⁰ Oblicz pole przekroju ostrosłupa płaszczyzną wyznaczoną przez środki krawędzi AB i BC oraz wierzchłek S

Michał: może ktoś narysuje wykres

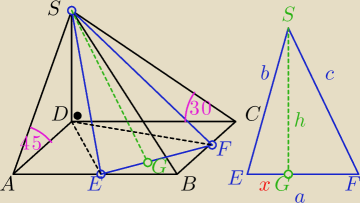
dero2005: W tej chwili nie mogę zrobić rysunku, spróbuję opisać. Oznaczamy podstawę jakoABCD i wierzchołek S. Odcinek DS = H jest prostopadłym do podstawy. Odcinek SC jest nachylony do podstawy pod kątem 30^o, odcinek AS jest nachylony do podstawy pod kątem 45^o, trzecią krawędzią boczną jest odcinek BS. W połowie odcinka AB zaczymy punkt E a w połowie odcinka BC punkt F. Łączymy punkty EFS. i mamy trójkąt, który jest obrazem przekroju płaszczyzną. Mamy dane H Liczymy odcinek CD

	H
CD =		= H√3
	tg30

Liczymy odcinek AD

	H
AD =		= H
	tg45

Liczymy odcinek CF

	AD		H
CF = FB=		=
	2		2

Liczymy odcinek EB

	CD		H
EB = EA =		=		√3
	2		2

Liczymy odcinek FD

	H
FD = √DC2 + FC2 =		√13
	2

Liczymy odcinek ED

	H
ED = √AD2 + AE2 =		√7
	2

Liczymy odcinek FS

	H
FS = √H2 + DF2 =		√17
	2

Liczymy odcinek ES

	H
ES = √H2 + DE2 =		√11
	2

Liczymy odcinek FE

	H
FE = √EB2 + BF2 =		√7
	2

Mamy policzony trójkąt EFS Oznaczmy bok EF −a, ES − b ,FS − c, z punktu S poprowadźmy wysokość h do przecięcia się z podstawą trójkąta (bokiem a) w punkcie G, oznaczamy odcinek EG jako x Układamy układ równań x² + h² = b² (a − x)² + h² = c² Liczymy x, h

	a*h
P =		=
	2

dero2005:

Michał: jeszcze raz napisze treść zadania Podstawą ostrosłupa jest prostaką ABSD Krawędż boczna DS jest prostopadła do płaszczyzny podstawy i ma długość H Ściana ABS nachylona jest do płaszczyzny podstawy pod kątem o mierze 45⁰ a ściana BCS pod kątem o mierze 30⁰ Oblicz pole przekroju ostrosłupa płaszczyzną wyznaczoną przez środki krawędzi AB i BC oraz wierzchołek S według Twojego rysunku Ściana ABS nachylona jest do płaszczyzny podstawy pod kątem o mierze 45⁰ to kąt DES = 45⁰ ściana BCS pod kątem o mierze 30⁰ to kąt SFD = 30⁰ nie wiem czy te kąty to te same które są wyznaczone na rysunku

Michał:

	1
zapomiałem dopisać że wynik to P =		*H2 √13
	4

dero2005: kąt DES ≠ 45^o kąt DFS ≠ 30^o

Michał: ale w zadaniu jest polecenie że ściana ABS nachylona jest do płaszczyzny podstawy pod kątem 45⁰ a z rysunku kąt DAS = 45⁰ to kąt nachylenia krawędzi AS do krawędzi podstawy AD chyba że się mylę

Michał: rozwiązując twój układ równań x² + h² = b² (a − x)² + h² = c² nie otrzymałem wyniku

dero2005: Znalazłem jeden błąd FE = H Wynik wyszedł mi

	H2
P =		√43
	8

Michał: ale ten wynik jest niezgodny z

	1
P =		*H2 √13
	4

może te kąty są jednak nieprawidłowe bo te ściany są nachylone do płaszczyny podstawy a nie do krawędzi podstawy tak jak obrazuje rysunek z 18:41

Michał: ale ten wynik jest niezgodny z

	1
P =		*H2 √13
	4

może te kąty są jednak nieprawidłowe bo te ściany są nachylone do płaszczyny podstawy a nie do krawędzi podstawy tak jak obrazuje rysunek z 18:41

dero2005: Kąty są zaznaczone prawidłowo, bo krawędź podstawy i podstawa leżą w jednej płaszczyźnie. Spróbuj wysłac jeszcze raz ten wątek, może ktoś lepiej rozwiąże, sam jestem ciekawy.

prosta: Ten sposób liczenia pola trójkąta − układ równań−jest skuteczny, gdy wysokość h poprowadzimy do najdłuższego boku.... (w innym wypadku należy sprawdzić, czy trójkąt jest ostrokątny czy rozwartokątny i uwzględnić to w obliczeniach)

prosta: https://matematykaszkolna.pl/forum/282214.html

dero2005: czyli jednak mój wynik potwierdza się, trójkąt jest rozwartokątny, przy liczeniu tym sposobem x może wyjśc ujemne.

Michał:

	1
przeanalizowałem wszystkie oblicznia i pole jest równe P =		*H2 √43
	8

dziękuję bardzo wszystkim

dero2005: