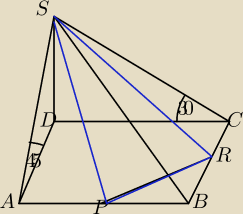
stereometria Wit: Witajcie w to niedzielne popołudnie To znowu ja z zadaniem, które mi sprawia trudność. Podstawą ostrosłupa jest prostokąt ABCD. Krawędź boczna DS jest prostopadła do płaszczyzny podstawy i ma długość H. Ściana ABS nachylona jest do płaszczyzny podstawy pod kątem o mierze 45 stopni, a ściana BCS pod kątem o mierze 30 stopni. Oblicz pole przekroju ostrosłupa płaszczyzną wyznaczoną przez środki krawędzi AB i BC oraz wierzchołek S. Obliczyłam niby, ale źle... Może zacznę od rysunku, bo pewnie już na początku tkwi błąd. To naprowadzicie mnie na to, co jest źle. Policzyłam z tego wszystkie boki przekroju, potem cosinus kąta PSR i z tego pole z użyciem boku boku i sinusa, tylko że widocznie błąd jest gdzieś dużo wcześniej...

Kinia: Jeeejku, nie rozumiem, czemu mi nick zmieniło na początek przywitania może kursor mi sam przejechał .

Kinia:

Kinia: Czy ten rysunek jest chociaż okej?

prosta: rysunek całkiem dobry, metoda też ok....le wyszło przy obliczeniach...i jaka jest odpowiedź? Ale jak wykorzystałaś nachylenie ściany do płaszczyzny podstawy?

prosta: Podstawa ma boki: H oraz H√3

Kinia: Tak, takie boki podstawy miałam właśnie, wykorzystałam tak, że wszystkie ściany boczne są trójkątami prostokątnymi i z trójkątów 45,90,45 oraz 30,60,90 obliczyłam szukane krawędzie boczne i potem mogłam obliczyć boki przekroju, a podstawa przekroju mi wyszła H.

	1
Odpowiedź jest taka:		H2√13
	4

Ja miałam "brzydkie" pierwiastki w tej mojej metodzie...

prosta: a boki przekroju jak wyszły? Porównajmy

Kinia:

	H*√17
Hm.. miałam to ołówkiem i zmazałam już, ale o ile pamiętam to jeden		a drugi
	2

podobnie tylko pierwiastek z 11 był.

prosta: też tak mi wyszło...trzeci H

Kinia: No tak , czyli albo się pomyliłam gdzieś dalej albo ja nie wiem.. Kurczę, ale skoro było dobrze, to mogłam nie mazać

prosta: tutaj inne sposoby liczenia pola przekroju : https://matematykaszkolna.pl/forum/281754.html

Kinia: uuuuaaa, Heronem

Kinia: prosta a liczyłaś to może? Wychodzi tak jak chcą w odpowiedziach?

prosta: albo przez obl. wysokości opuszczonej na najdłuższy bok....można tak sprawdzić siebie drugą metodą.... też nie otrzymałam takiego wyniku jak w odp. zaraz posprawdzam

prosta: Dwiema różnymi metodami mam:

	√43
Pole=		H2
	8

Kinia: Hm.. może jest błąd w książce? Nie mam pojęcia, ale denerwuje mnie to, że namęczę się nad jakimś zadaniem, w miarę dobrze je wykonuję, potem sprawdzam − źle, to zmazuję i od nowa... dodatkowo pytam tutaj, a potem okazuje się, że było dobrze. To smutne

prosta: róne psikusy nam się zdarzają....nie zmazuj, tylko sprawdź gdzieś na boku dodatkowo, skonsultuj i w ostateczności wymaż pierwsze obliczenia

prosta: jak widać wyniki nie zawsze piękne wychodzą

Kinia: No pewnie tak, masz rację, mam nauczkę na przyszłość i dziękuję za zaangażowanie i pomoc

Kinia: no i zrobiłam od nowa i nie mam nawet takiego wyniku jak Ty, czyli dalej coś robię źle... a jaki masz cosα? Biorąc pod uwagę, że alfa to ten kąt przy wierzchołku S

Kinia: albo sinα od razu? nie wiem gdzie mam błąd ...

Bogdan:

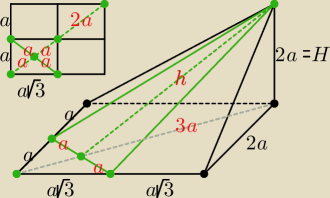
	1
H = 2a ⇒ a =		H h = √4a2 + 9a2 = a√13
	2

	1
Pole przekroju P = a*h = a*a√13 = a2√13 =		H2√13
	4

początki: Bogdan mógłbyś mi sprawdzić zad. z trygonometrii ? Bo nawet nie wiem czy dobrze zaczęte jest ?

prosta: tak analizuję to rozwiązanie i zastanawiam się skąd pewność, że przekrój to trójkąt równoramienny?

prosta: wydaje mi się, że to nie jest trójkąt równoramienny i nie możemy przyjąć takiego położenia wysokości h,

Bogdan: rzeczywiście, przekrój nie jest trójkątem równoramiennym, mój rysunek zawiera błędnie położoną wysokość h

prosta: tak byłoby gdyby podstawa była kwadratem

prosta:

	12
cosα=
	√11*17

	√43
sinα=
	√11*17

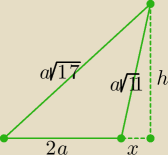
Bogdan: No to jeszcze raz H = 2a

	1		1
h2 + x2 = 11a2 i h2 + (2a + x)2 = 17a2 stąd x =		a i h =		a√43
	2		2

	1		1		1		1
Pole przekroju P =		*2a*h = a*		a√43 =		a2√43 =		H2√43
	2		2		2		8

prosta: Dzięki, −−− potwierdza to moje obliczenia

prosta: ja liczyłam w ten sposób ...tylko szukałam najkrótszej wysokości − opuszczonej na najdłuższy bok

Bogdan: Ja również dziękuje za zwrócenie mi uwagi o błędnie przyjętym założeniu, że badany trójkąt jest równoramienny

Kinia: Okej, sinus i cosinus miałam taki sam jak Ty prosta, tylko ja usuwałam niewymierność z mianownika i potem miałam pod pierwiastkiem w końcowym wyniku wielkie liczby Dziękuję Wam obu za pomoc

Kinia: Nie no, ja nie wytrzymam, mam kolejne zadanie które mi nie wyszło i nie widzę błędu znowu Odpowiedzi podają coś innego, chociaż w tym przypadku zbliżone do mojego wyniku. Nie wiem czy ktoś to zechce przeczytać, a co dopiero sprawdzić, ale pomóżcie po raz kolejny biednej maturzystce, to zadanie za 7 pkt więc chciałabym wiedzieć, czy mi wyszło, czy może jednak nie. Treść: Wyznacz p∊R, dla którego suma sześcianów pierwiastków równania x² + (p−3)x + p² = 0 jest największa i oblicz jej wartość. Moje rozwiązanie (w skrócie) Δ=−3(p²+2p−3) Δ>0 ... Z tego założenia wychodzi: p∊(−3,1) Teraz: x₁³ + x₂³ = (x₁+x₂)[(x₁+x₂)² −3x₁x₂] = ... = 2p³ − 27p +27 = f(p) Obliczam f'(p) = 6p² − 27 Δ=648 √Δ = 18√2 p₁ = −1,5√2 p₂ = 1,5√2 rysuję wykres znaku pochodnej pamiętając o tym, że p∊(−3,1) Sporządzam tabelkę z które wychodzi mi, że funkcja f(p) przyjmuje największą wartość dla p=−1,5√2 To jest pierwsza część odpowiedzi. Teraz druga: Liczę f(−1,5√2)=...=27(√2 +1)

	−3
Oni podają, że największa wartość jest dla p=
	2

zyd: a tak z ciekawośći dlaczego w pochodnej liczyłaś Δ ?

zyd:

Kinia: żeby znaleźć tego miejsca zerowe

Kinia: A dobrze jest chociaż?

zyd: czas na maturze jest bardzo cenny więc liczenie w takich przypadkach delty jest czasochłonne więc lepiej 6p² − 27 = 0

zyd: mowia Ci coś wzory vieta ..

Kinia: ok, zapamiętam dzięki za wskazówkę

Kinia: No to przecież ich użyłam! Zrobiłam w nich błąd czy co?

zyd: takie mam przeczucie że tam się pomyliłaś

Kinia: Przeczucie to wiesz ja mam inne, że się nie pomyliłam i szukam pewności gdzie jest błąd

prosta: gdzie podają takie odpowiedzi?

Kinia: Arkusze maturalne z matematyki poziom rozszerzony "To nie takie trudne" wyd. Dla Szkoły

Jankes: tvn szkołą wydała książke pewnie smoczyca ją napisała nie moge się powstrzymac przed rozwazaniem tego zdania poczekaj chwilke

Jankes: ok już mi wyszło −1.5

Kinia: Więc gdzie ten błąd, dowiem się w końcu?

Jankes: kapcza

Kinia: a bardziej zrozumiale?

Krab: Up

Krab: rozwiaze nam to ktos?