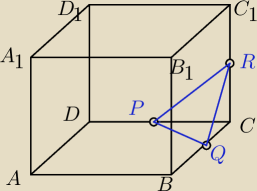
Oblicz pole trójkąta PQR Aga: Dany jest prostopadłościan, w którym |BC|=6, |DC|=8, |CC₁|=24. Punkty P, Q i R są środkami odpowiednich krawędzi prostopadłościanu. ( punkt P jest środkiem boku |CD|, punkt Q jest środkiem boku |BC|, punkt R jest środkiem boku |CC₁|. Oblicz pole trójkąta PQR.

dero2005: Narysuj rysunek, zaznacz punkty jak w zadaniu, policz długości odcinków PR, QR, PQ z Pitagorasa i policz pole trójkąta z wzoru Herona

dero2005:

Aga: Zrobiłam rysunek, policzyłam za pomocą Pitagorasa te odcinki, policzyłam pole, ale nie że wzoru Herona. Niestety pomimo kilka kostnego przeliczenia wyszła mi odpowiedź niezgodna z kluczem odpowiedzi do zadań (wynik podany przez autora z tyłu książki).

dero2005: jaka jest odpowiedź?

Aga: 6 pierwiastków z 26

dero2005: Policz pole z wzoru Herona i wyjdzie dobrze

zuza: z − odcinek od P do Q 3² + 4² = z² 9 + 16 = z² 25 = z² z = 5 y − odcinek od P do R 4² + 12² = y² 16 + 144 = y² 160 = y² y = 4 pierwiastki z 10

dero2005: Licz dalej to wyjdzie jak w odpowiedzi

Aga: Mam problem z bokiem |QR|, bo : y=4 pierwiastki z 10 z=5 z²+y²= x² Wychodzi mi pierwiastek z 185 A jak liczę 3²+12²=z² To mi wychodzi pierwiastek z 153 Zgubiłam się. Nie rozumiem tego zadania. Robię go 3 dzień chyba 😂

Rene: Rozwiązywałam również to zadanie i ze wzoru Herona przy bokach: 5 4 pierwiastki z 10 pierwiastek z 153 wychodzą mi kosmiczne liczby, aż się gubię... Dlatego jeśli ktoś umie to rozwiązać to błagam napiszcie od początku do końca całe rozwiązanie tego zadania

dero2005: jeżeli wykażecie trochę cierpliwości to postaram się to napisać

dero2005: RC = 12 PC = 4 CQ = 3 RQ = √12² + 3² = √144+9 = √153 = 3√17 PQ = √3² + 4² = √9+16 = √25 = 5 RP = √12² + 4² = √144+16 = √160 = 4√10 RQ = a = 3√17 PQ = b = 5 RP = c = 4√10 dla przejrzystości będę liczył częściami S = √p(p−a)(p−b)(p−c)

	a+c+b		3√17+4√10+5
p =		=
	2		2

	3√17+4√10+5		6√17		4√10+5−3√17
(p−a) =		−		=
	2		2		2

	3√17+4√10+5		10		3√17+4√10−5
(p−b) =		−		=
	2		2		2

	3√17+4√10+5		8√10		3√17−4√10+5
(p−c) =		−		=
	2		2		2

	4√10+5−3√1		3√17+4√10−5
(p−a)(p−b) =		*		=
	2		2

	12√170+160−20√10+15√17+20√10−25−153−12√170+15√17
=		=
	4

	30√17−18
=
	4

	30√17−18		3√17−4√10+5
[(p−a)(p−b)][(p−c)] =		*		=
	4		2

	1530−120√170+150√17−54√17+72√10−90
=		=
	8

	1440−120√170+96√17+72√10
=
	8

	3√17+4√10+5		1440−120√170+96√17+72√10
p[(p−a)(p−b)(p−c)] =		*		=
	2		8

	4320√17−360√2890+4896+216√170+5760√10−480√1700
=		+
	16

	384√170+2880+7200−600√170+480√17+360√10
+		=
	16

	4800√17+6120√10−360√2890−480√1700+14976
=		=
	16

	4800√17+6120√10−6120√10−4800√17+14976
=		=
	16

	14976
=		= 936
	16

√936 = 6√26 = S

prosta: można też poprowadzić wysokość na najdłuższy bok c i budować układ równań stosując tw. Pitagorasa w powstałych trójkątach: a=√153=3√17 , b=3, c=√160=4√10

⎧	x 2+h2=a2
⎩	h2+(c−x)2=b2

	a2+c2−b2
x=
	2c

	36		3√26
x=		⇒ h=
	√10		√10

	1		1		3√26
P=		ch=		*4√10*		=6√26
	2		2		√10