... Phoebe Campbell: Muszę rozwiązać równanie |x−1|+|x+3|=4 Zacząłem od ustalania przedziałów x−1≥0 → x∊<1;∞) x+3≥0 → x∊<−3;∞) x∊(−3;1) Mam problem z 2 przedziałem w przypadku |x−1|, gdy podstawię −3 będzie wartość ujemna, a gdy podstawię np. 1000 będzie dodatnia.. więc nie wiem czy mam opuścić wartość bezwzględną czy wszystko *−1 zrobić..

Metis: |x−1|+|x+3|=4 1) x∊(−∞,−3) 2) x∊[−3,1) 3) x∊[1,+∞)

Phoebe Campbell: Jak to otrzymałeś?

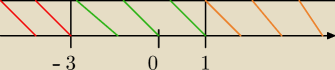
Metis: x−1=0 x=1 x+3=0 x=−3

5-latek: https://matematykaszkolna.pl/strona/1796.html np tak

Phoebe Campbell: Czyli mając 2 wartości bezwzględne wyliczam wartość zmiennej dla każdej przyrównując do zera, zaznaczam 2 pkty na osi i robię z tego 3 przedziały?

Phoebe Campbell: 5−latek − właśnie według tego próbowałem i coś mi nie wyszło

5-latek: Tak wlasnie robisz . Liczba przedzialow jest o 1 wieksza niz liczba modulow

Phoebe Campbell: okej.. pytanie jeszcze tylko czy każdy pkt. który zaznaczę na osi (mam na myśli w tym przypadku −3 i 1) ma "zamalowaną" kropkę?

Metis: To równość

Phoebe Campbell: No tak, ale to się przekłada potem na przedziały, a w nich muszę zaznaczyć czy są otwarte czy zamknięte co z resztą sam zrobiłeś

Phoebe Campbell: To jak z tymi przedziałami? Skąd mam wiedzieć czy są otwarte czy zamknięte? Mam jeszcze sporo zadań tego typu, a bez tej wiedzy daleko nie zajadę

Metis: Skoro w jednym przedziale włączasz liczbę do drugim już tego nie robisz...

Phoebe Campbell: Czyli to nie ma znaczenia w którym włączę.. byleby w drugim przedział był otwarty?

Metis: Jedziesz po kolei. Np: |x+2|+|x+3|+|x−1|+|x−5|=0 −2, −3,1, 5 porządkujesz rosnąco −3,−2,1,5 x∊(−∞,−3) − otwarty tu zamykam x∊[−3,−2) − otwarty tu zamykam x∊[−2,1) − otwarty tu zamykam x∊[1,5) − otwarty tu zamykam x∊[5,+∞) − otwarty

5-latek: Tak

Phoebe Campbell: Dzięki serdeczne za pomoc. Porobię trochę zadań.. zobaczymy co z tego wyjdzie.

PW: Pomyśl jutro nad tym: 279886. Przedział jest inny, ale filozofia ta sama.

Phoebe Campbell: Dzięki PW za link i odpowiedź w moim − innym − temacie. Wracając jeszcze do |x−1|+|x+3|=4.. dla przedziału (−∞;−3) pierwszą wartość bezwzględną zamieniłem na nawias z minusem z przodu bo zawsze wychodzi ujemna, ale druga wartość bezwzględna czyli |x+3| dla np. x=−100 będzie ujemna, ale dla x=−2,9 będzie dodatnia.. więc nie wiem co z tym zrobić..

PW: Jeżeli upierasz się, żeby "rozbijać na przedziały", to dobrze jest zacząć od narysowania miejsc zerowych "poszczególnych modułów" na osi. Zobaczyłbyś wtedy bez takich wątpliwości, że −3 < −2,9, a więc nie ma co się trapić, liczba (−2,9) należy już do następnego przedziału (nie jest elementem przedziału (−∞, −3)).