 Nalepiej to narysowac sobie wykres tej funkcji Gniewna Damo
Nalepiej to narysowac sobie wykres tej funkcji Gniewna Damo  Widzimy juz co mamy liczyc .
A obliczyc to juz latwo bo musimy rozwazac podwojna nierownosc 1≤3x2<9 i wyznaczyc czesc
wsppolna rozwiazan
czyli masz rozwiazc dwie nierownosci 3x2<9 i 3x2≥1
Widzimy juz co mamy liczyc .
A obliczyc to juz latwo bo musimy rozwazac podwojna nierownosc 1≤3x2<9 i wyznaczyc czesc
wsppolna rozwiazan
czyli masz rozwiazc dwie nierownosci 3x2<9 i 3x2≥1

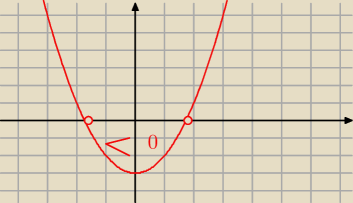 No nie moja Damo
3x2<9 to 3x2−9<0 to x2−3<0 to x=√3 lub x= −√3 ale ze to jest nierownosc a nie
rownanie to rozwiazniem tej nierownosci bedzie przedzial xnalezy (−√3,√3)
to jest wykres funkcji y=x2−3=0
No nie moja Damo
3x2<9 to 3x2−9<0 to x2−3<0 to x=√3 lub x= −√3 ale ze to jest nierownosc a nie
rownanie to rozwiazniem tej nierownosci bedzie przedzial xnalezy (−√3,√3)
to jest wykres funkcji y=x2−3=0

| 1 | ||
x2− | ≥0 | |
| 3 |
| √3 | √3 | |||
(x− | )(x+ | )≥0 | ||
| 3 | 3 |
 Druga nierownosc 3x2≥1 to 3x2−1≥0 i musimy rozwiazc taka nierownosc Wyznaczymy miejsca
Druga nierownosc 3x2≥1 to 3x2−1≥0 i musimy rozwiazc taka nierownosc Wyznaczymy miejsca
| 1 | 1 | 1 | √3 | |||||
zerowe to x2= | to x=√ | = | = | (po usunieviu niewymiernosci z | ||||
| 3 | 3 | √3 | 3 |
| 1 | √3 | |||
mianownika lub x=−√ | =− | Teraz w zwiazku z tym ze to niejest rownianie tylko | ||
| 3 | 3 |
| √3 | √3 | |||
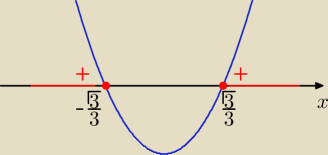
nierownosc slaba Widzimy ze 3x2−1≥0 dla xe(−oo,− | >U<p | ,oo) | ||
| 3 | 3 |




| a | √a | |||
Popatrz mamy tak √ | = | czyli mozemy zapisac tak | ||
| b | √b |
| 1 | √1 | 1 | ||||
√ | = | = | bo √1=1 | |||
| 3 | √3 | √3 |
| 1 | √3 | √3 | ||||
Teraz | * | = | ||||
| √3 | √3 | 3 |
 Pozdrawiam
Za dlugo i za duzo piszse
Pozdrawiam
Za dlugo i za duzo piszse 