zadanko Bezgłowy matematyk : W trójkącie ABC wierzchołki mają współrzędne A(−7,−1), B(−1,−3), C(−5,1). a) wykaż, że trójkąt ABC jest prostokątny b) oblicz pole trojkąta ABC c) oblicz pole koła opisanego a trójkącie ABC d) napisz równanie prostej, w ktorej zawiera się środkowa CD...

PW: a) Policz długości boków i skorzystaj z twierdzenia odwrotnego do twierdzenia Pitagorasa. b) Połowa iloczynu przyprostokątnych c) Promień koła opisanego to połowa przeciwprostokątnej.

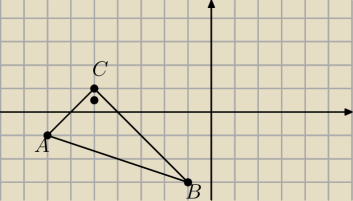
Metis: a) Np, tak. Liczymy współrzędne wektorów [AC] i [BC]. [CA]=[−5+7,1+1]=[2,2] [CB]=[−5+1, 1+3]=[−4,4] Ze wzoru na iloczyn skalarny można wyprowadzić wzór na cosinus kąta między wektorami:

	aob
cosα =
	|a|*|b|

https://matematykaszkolna.pl/strona/1630.html Liczymy zatem iloczyn skalarny wektorów [CA], [CB]... [CA]o[CB]=2*(−4)+2*4=−8+8=0 Podstawiając do wzoru:

	[CA]o[CB]
cosα =
	|[CA]|*|[CB]|

	0
cosα =
	|[CA]|*|[CB]|

cosα=0 Funkcja cosinus jest równa 0, gdy α=90^o , zatem wektory [CA] i [CB] tworzą kąt prosty, co oznacza, że trójkąt ABC jest prostokątny.

Mila: Wystarczy obliczyć iloczyn skalarny: [CA]o[CB]=0⇔CA⊥CB

Gustlik: A(−7,−1), B(−1,−3), C(−5,1). a) wykaż, że trójkąt ABC jest prostokątny Liczę wektory kierunkowe wszystkich boków i ich współczynniki kierunkowe:

	2		1
AB→=[−1−(−7), −3−(−1)]=[6, −2], a1=−		=−
	6		3

	2
AC→=[−5−(−7), 1−(−1)]=[2, 2], a2=		=1
	2

	4
BC→=[−5−(−1), 1−(−3)]=[−4, 4], a3=		=−1
	−4

AC^→⊥BC^→ ⇒ Δ jest prostokatny, kąt C jest prosty b) oblicz pole trojkąta ABC Z wyznacznika wektorów: d(AB^→, AC^→)= | 6 −2 | | 2 2 | =6*2−(−2)*2=12+4=16

	1		1
Odp: P=		|d(AB→, AC→)|=		*|16|=8
	2		2

c) oblicz pole koła opisanego a trójkącie ABC Kąt C jest prosty (pkt. a), zatem AB jest przeciwprostokątną |AB^→|=√6²+(−2)²=√36+4=√40=2√10

	1
r=		*|AB→|=√10
	2

Odp: P=πr²=10π d) napisz równanie prostej, w ktorej zawiera się środkowa CD... A(−7,−1), B(−1,−3), C(−5,1).

	−7+(−1)		−1+(−3)		−8		−4
D=SAB=(		,		)=(		,		)=(−4, −2)
	2		2		2		2

C=(−5,1) D=(−4, −2) Liczę wektor kierunkowy:

	−3
CD→=[−4−(−5), −2−1]=[1, −3], a=		=−3
	1

y=−3x+b 1=−3*(−5)+b 1=15+b b=−14 Odp: y=−3x−14

Bezgłowy matematyk : Dzięki wielkie