 Witam,
Robiłem próbną maturę z zadania.info i mam pytanie odnośnie jednego rozwiązania. Czy moje
rozumowanie jest poprawne?
Oto treść zadania:
Wykaż, że jeżeli α≤β≤γ są kątami wewnętrznymi trójkąta rozwartokątnego, to:
sin2α<sin2γ−sin2β
(tak, wiem, aż się nasuwa, wykorzystać twierdzenie sinusów, ale nie wpadłem na to)
sin2α<(sinγ−sinβ)(sinγ+sinβ)
Witam,
Robiłem próbną maturę z zadania.info i mam pytanie odnośnie jednego rozwiązania. Czy moje
rozumowanie jest poprawne?
Oto treść zadania:
Wykaż, że jeżeli α≤β≤γ są kątami wewnętrznymi trójkąta rozwartokątnego, to:
sin2α<sin2γ−sin2β
(tak, wiem, aż się nasuwa, wykorzystać twierdzenie sinusów, ale nie wpadłem na to)
sin2α<(sinγ−sinβ)(sinγ+sinβ)
| γ−β | γ+β | γ+β | γ−β | |||||
sin2(γ+β)<(2sin | cos | )(2sin | cos | ) | | ||||
| 2 | 2 | 2 | 2 |

 Michał staraj się przeprowadzać dowody zaczynając od założenia, nie od tezy.
Zał.
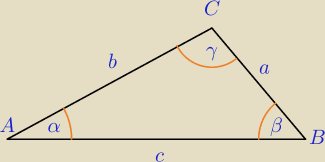
α≤β≤γ są kątami wewnętrznymi trójkąta rozwartokątnego,
T. to:
sin2α<sin2γ−sin2β
D.
ΔABC− Δrozwartokątny ( z zał.)⇔
(*) c2>a2+b2
Z tw sinusów:
Michał staraj się przeprowadzać dowody zaczynając od założenia, nie od tezy.
Zał.
α≤β≤γ są kątami wewnętrznymi trójkąta rozwartokątnego,
T. to:
sin2α<sin2γ−sin2β
D.
ΔABC− Δrozwartokątny ( z zał.)⇔
(*) c2>a2+b2
Z tw sinusów:
| a | |
=2R⇔a=2R*sinα | |
| sinα |
| b | |
=2R⇔b=2R*sinβ | |
| sinβ |
| c | |
=2R⇔c=2R*sinγ | |
| sinγ |
